前回の記事は”Jane Street Market Prediction”のデータに全体の特徴について簡単に見ました。
そこでは、リターンと特徴量では相関が低いものの、各特徴量では相関が高いものがあることがわかりました。しかし、特徴量の数が130個あり、リターン(resp)との関係を把握するには苦しい状況でした。
そこで今回は、特徴量の次元を圧縮し、各クラスタごとにrespとの関係を調べてみます。
次元圧縮には、主成分分析とクラスタリング(K-means)を用いてみます。
※本記事は、公開しているNotebookをまとめたものとなっております。
データの標準化
まずは、データを標準化します。
前回の分析では、標準化はしておりませんが結果は大差なかったです。
標準化には、scikit-learnのpreprocessing.StandartScaler()を利用します。
尚、テストデータも同じパラメータで標準化を行うので、学習データ使用したインスタンスも保存しておきます。
また、今回の学習データとテストデータはデータの形状が異なるので、学習データのデータフレームをテストデータと同じ形状に統一しておきます。
合わせて、respに関する情報を1オブジェクトにまとめ保存しておきます。
import numpy as np
import pandas as pd
import pickle
# read data
train = pd.read_csv('/kaggle/input/jane-street-market-prediction/train.csv')
test = pd.read_csv('/kaggle/input/jane-street-market-prediction/example_test.csv')
# 欠損値の補完(前の値で補完する)
train.fillna(method = 'ffill', inplace=True)
train.dropna(inplace=True)
# respについて
resp_params = (train['resp'].mean(), train['resp'].std())
resp_standardized = ((train['resp'] - resp_params[0])/resp_params[1]).values
resp_info = (resp_params, resp_standardized)
# 基準化
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit(train[test.columns])
Z = sc.transform(train[test.columns])
train = pd.DataFrame(Z, columns=test.columns) # dfの整形
train = reduce_mem_usage(train) # メモリ対策(関数は前回の記事参照)
# 保存
import pickle
train.to_pickle('/kaggle/working/train_standardized_without_null.pickle')
with open('/kaggle/working/SC.pickle', 'wb') as f:
pickle.dump(sc, f)
with open('/kaggle/working/resp_info.pickle', 'wb') as f:
pickle.dump(resp_info, f)主成分分析(PCA)
特徴量(feature_X)について主成分分析を行い、累積寄与率をプロットしてみます。
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# 特徴量のみにする
X = train.drop(['weight', 'date', 'ts_id'],axis=1).values
# 主成分分析
pca = PCA()
pca.fit(X)
# データを主成分空間に写像(主成分スコア)
score = pca.transform(X)
# 累積寄与率を図示する
plt.plot([0] + list( np.cumsum(pca.explained_variance_ratio_)), "-o")
plt.xlabel("Number of principal components")
plt.ylabel("Cumulative contribution rate")
plt.grid()
plt.show()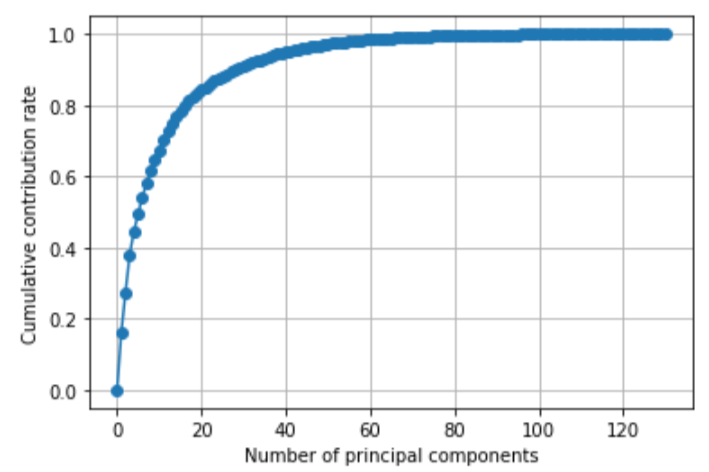
上図から概ね第30主成分程度で特徴量全体の90%を表現できていることがわかります。
ちゃんと調べてみたら第16主成分で80%、第20主成分で85%、第28主成分目で90%を上回っていました。
リターンと各主成分の関係
第16主成分までを取り出し、resp(リターン)や各主成分間の関係を見てみます。
import seaborn as sns
# respと主成分スコアの関係
# df作成
target = pd.DataFrame(np.concatenate([resp_info[1][:, np.newaxis], score[:, :16]], axis=1))
target.columns = pd.Index(['resp'] + ['PC{}'.format(i+1) for i in range(16)])
# ヒートマップ作成
sns.heatmap(target.corr())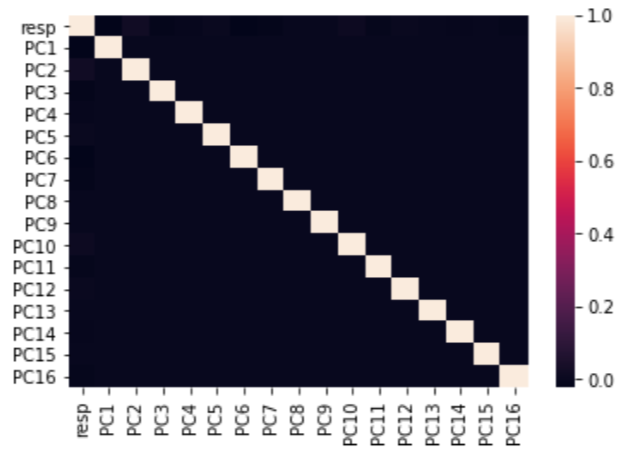
各主成分やrespの間に相関は低いことがわかる。
主成分回帰モデル(PCRモデル)
ひとまず、この16主成分でrespの線形モデルを作成し、テストデータのresp推定してみます。
import statsmodels.api as sm
# 'weight'を追加
target = pd.concat([target, train['weight']], axis=1).copy()
target.head()
# PCR
x = target.drop(['resp'], axis=1)
x = sm.add_constant(x)
model = sm.OLS(target['resp'], x)
result = model.fit()
print(result.summary())
# グラフを書く
plt.plot(target['resp'], label='resp', linestyle='--')
result.fittedvalues.plot(label='fitted', style=':')
plt.legend()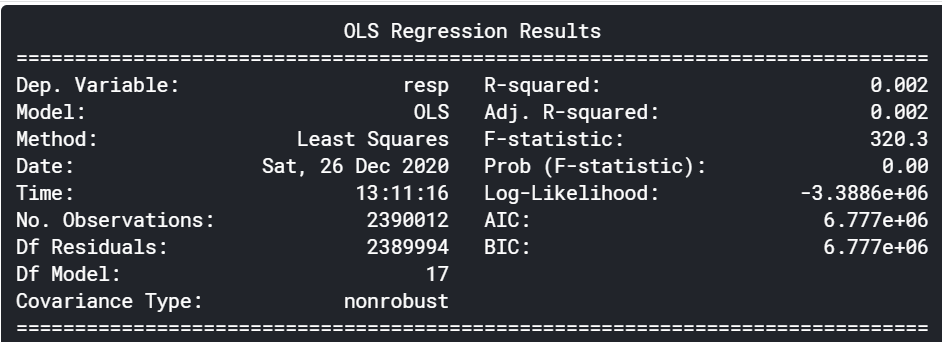
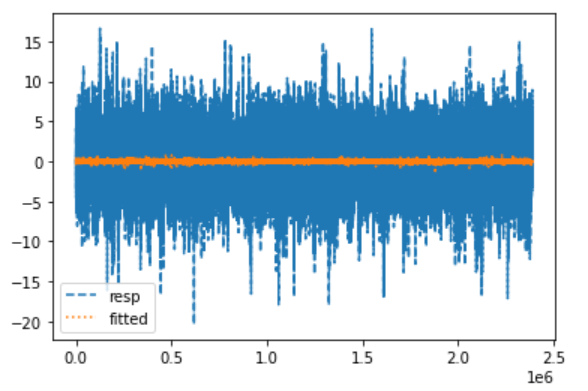
全期間で線形回帰を行った結果、決定係数は0.002と酷いです。
全期間のデータを使うのはよくなさそうです。(周期性などを考慮したほうが良いのかもしれない?)
次に、最初の100個を対象に最適化を行った結果は以下の通りです。
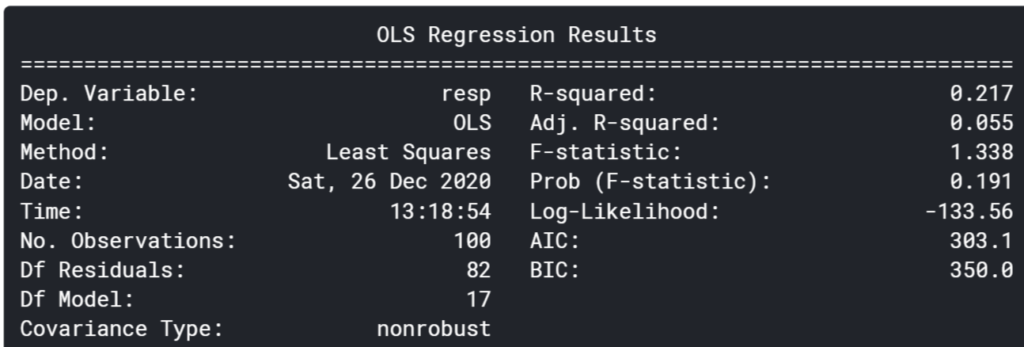
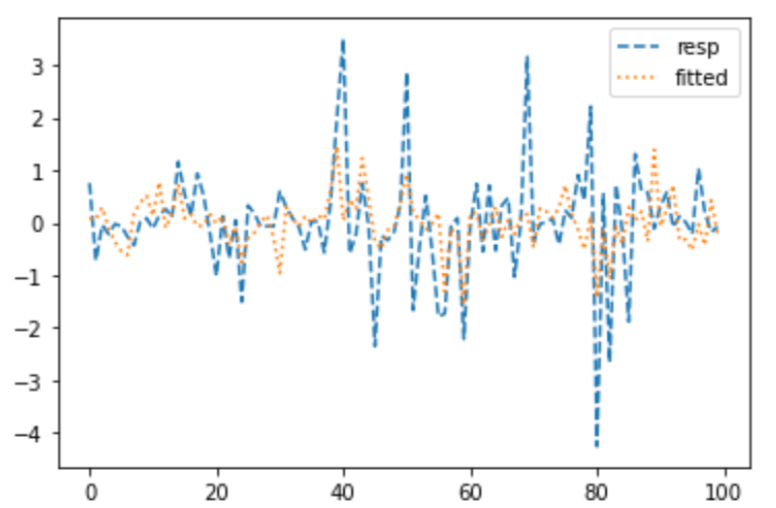
そこそこフィットしている様子が見られます。データを少なくすればフィットするようです。
期間を複数に分け、各期間ごとで最適なモデルを採用するようなものにすると良いのかもしれないです。
分析に入る前に、リターンの特徴(周期性など)を最初に見るべきだったかもしれないです。
クラスタリング(K-means)
主成分スコア(第16主成分まで)をクラスタリングし、各クラスタごとのリターンに特徴があるか見てみます。
from sklearn.cluster import KMeans # K-means
kmeans_model = KMeans(n_clusters=5, random_state=0).fit(target.iloc[:, 1:]) # resp以外
km_result = pd.concat([target, pd.DataFrame(kmeans_model.labels_, columns=['cluster'])],axis=1)
km_result.groupby('cluster').describe()['resp']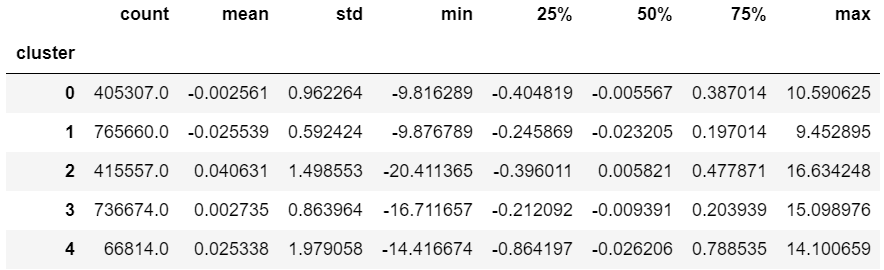
次にrespを正負に変換し、クラスタごとにカウントしてみます。
km_result['resp_pn'] = km_result['resp'].apply(lambda x:'p' if x>0 else 'n')
km_result.groupby(['cluster', 'resp_pn']).count()['resp'].plot.bar(color=['blue', 'red'])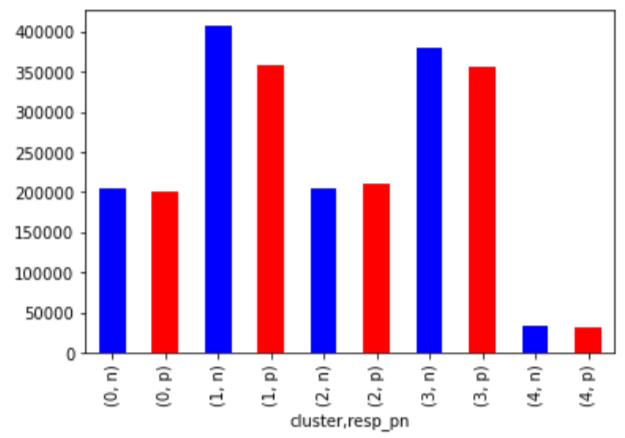
カウントベースでみると、クラスター1と3ではマイナスの方が数が多いことがわかります。
クラスター1については、平均もマイナスであり、マイナスの特性を持ちそうです。
クラスター数を3にしてみると以下の結果が得られました。
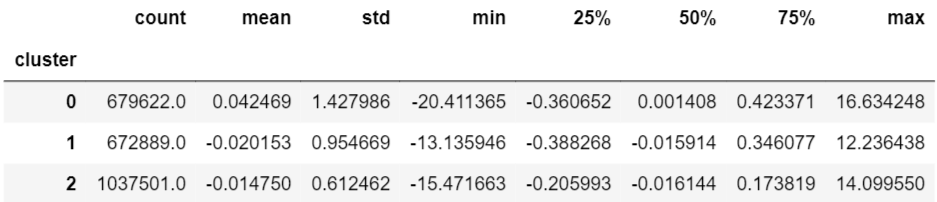
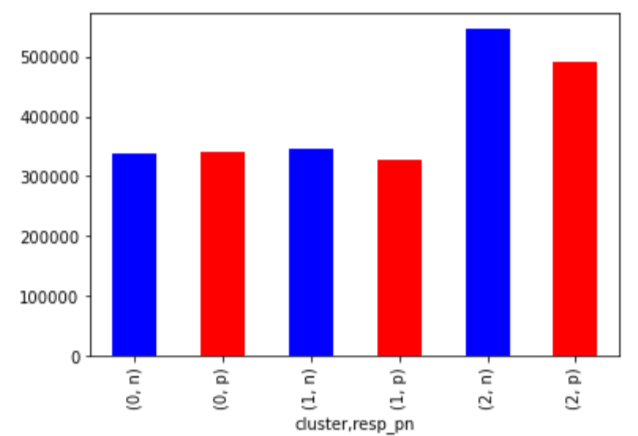
次にクラスター数を10にしてみた場合です。
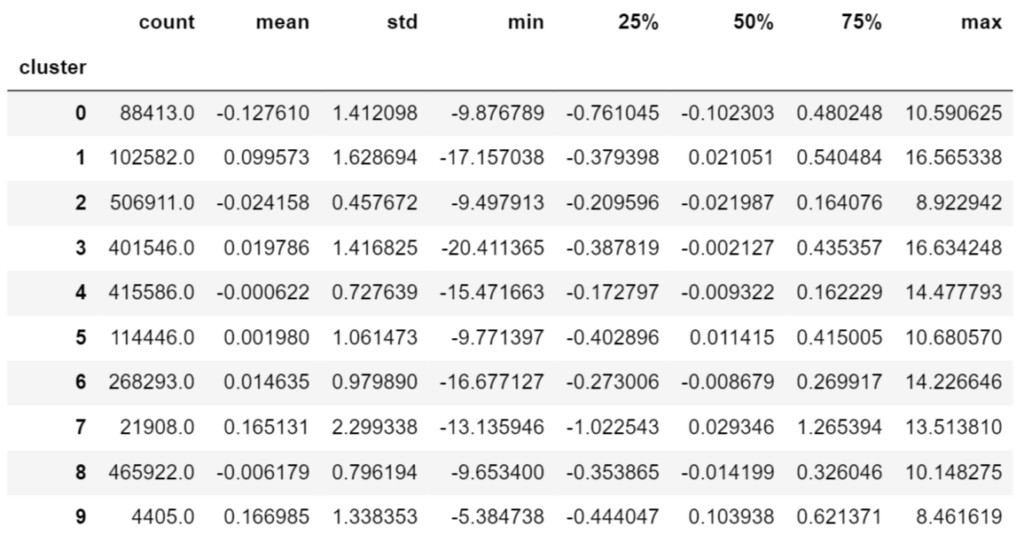
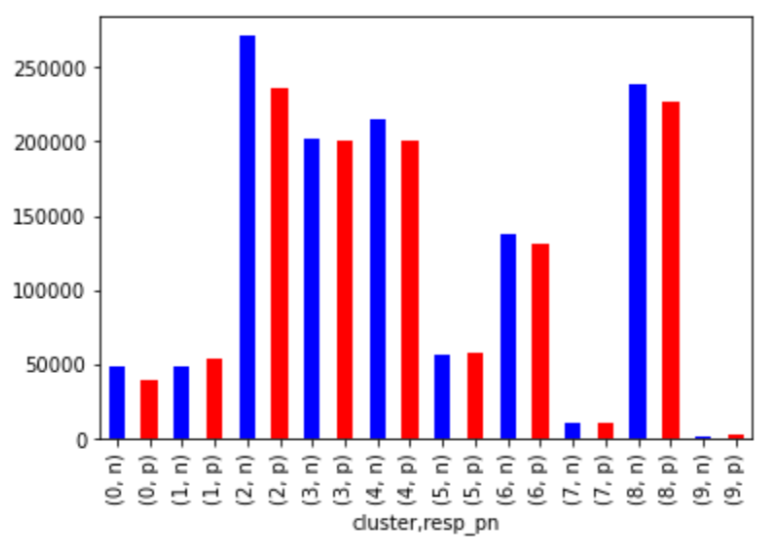
クラスターで分けることでマイナスの特徴を捉えることができている可能性があります。
また、クラスター数は、3程度でも十分と思われれます。
今回の結果を踏まえると、モデル開発においてクラスター番号を入れてみる価値はありそうです。
ただし、ポジティブの特徴について見ると、クラスター数5の(2,p)が捉えることができている可能性があるのを踏まえると、クラスター数は5としてみようと思います。
主成分分析+クラスタリング
上記で算出したクラスター番号を説明変数に追加し、線形回帰を行ってみます。
# PCR + Clustering
x = km_result.drop(['resp', 'resp_pn'], axis=1)
x = sm.add_constant(x)
model = sm.OLS(km_result['resp'][:100], x[:100])
result = model.fit()
print(result.summary())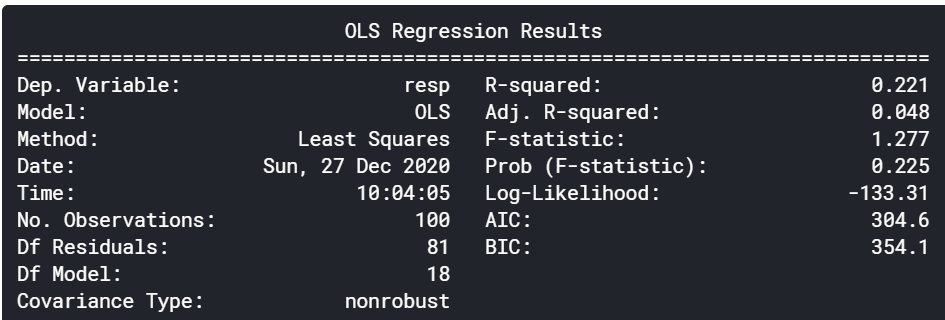
あまり改善はされませんでした。変数が一つ増えたことで、補正R2は低下しました。
そもそも主成分分析を行い、次元数を縮小させることに価値があるのか確認のため、元の特徴量(feature_X)で全期間に対して線形回帰を行ってみます。
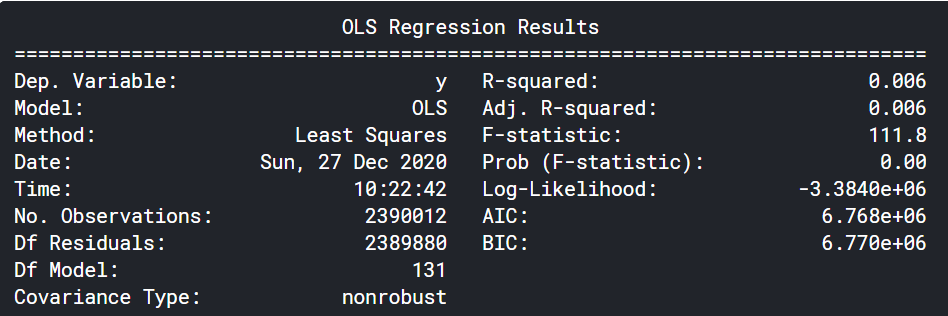
決定係数だけについて見てるとこちらのほうがフィットしています(大差はない)。
ここまでの結果を踏まえると主成分分析による次元圧縮では厳しいように感じます。
ただ、使い方次第では、意味があるかもしれないのでもう少し検討していきたいところです。
まとめ
今回は、特徴量について主成分分析により次元圧縮を行い、各主成分とresp(リターン)との関係について簡単に見てみました。
resp(リターン)の特徴(周期性はないか、定常過程か、等)を見ていかないとモデル構築へは進めないと思うので、次回はrespに的を絞って特徴を見ていきたいと思います。
ここまでの結果から、提供されたデータだけを使ってモデルを作るだけでは、良いモデルは作れなそうな印象を抱いております。提供されたデータの特徴を見て、そこから新たな変数を作るなどしていくらかのひねり(工夫)を加えていかないと駄目な気がしてます。


コメント