これまでの記事では、KaggleのAPIを用いたデータ取得方法やKaggle上のNotebookからデータセットをダウンロードせずに利用する方法について書きました。
今回は、”Jane Street Market Prediction”のデータ特性について簡単に見ていきます。
ちなみに、こういう作業のことをEDA(探索的データ解析)と言うそうです。
※本記事は、公開しているNotebookをまとめたものとなっております。
データの読込みとメモリの節約
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
pd.set_option('display.max_columns', 140) #最大表示列数の指定
import matplotlib.pyplot as plt# dfの各列の型を設定しメモリ軽減
def reduce_mem_usage(df, verbose=True):
numerics = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
start_mem = df.memory_usage().sum() / 1024**2
for col in df.columns:
col_type = df[col].dtypes
if col_type in numerics:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == 'int':
if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
end_mem = df.memory_usage().sum() / 1024**2
if verbose: print('Mem. usage decreased to {:5.2f} Mb ({:.1f}% reduction)'.format(end_mem, 100 * (start_mem - end_mem) / start_mem))
return dfcsvから読み込んだデータは、データ型を指定しないとint64, float64になります。
大量のデータを扱う場合は、それが原因でメモリ不足エラーになります。
上記の関数を使用することでそれぞれのデータ列に対して最適なデータ型を設定することができます。
# before
train = pd.read_csv('/kaggle/input/jane-street-market-prediction/train.csv')
train.info()
# after
train = reduce_mem_usage(train)
train.info()
# dfをpickleで保存
train.to_pickle('/kaggle/working/JSMP_train.pickle')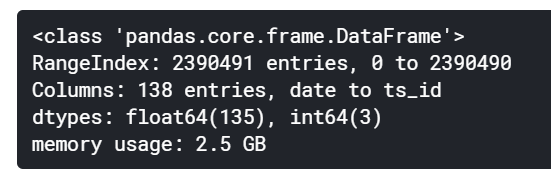
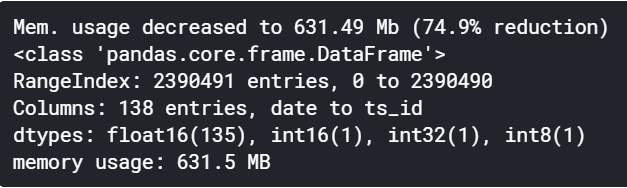
メモリ使用量を2.5GB⇒631.49MB(74.9%減)と大幅に節約することができました。
csvからデータを読み込むとかなり時間がかかるので、pickleで保存しておきます。
各特徴量の欠損値について
分析を始める前に、各特徴量の欠損値の数について見てみます。
null_num_train = {feature:num for feature, num in zip(train.columns, train.isnull().sum())}
print('max null ratio:', max(null_num_train.values()) /train.index.size)
print('null num:{}'.format(len([i for i in null_num_train.values() if i != 0])))
plt.figure()
plt.bar(null_num_train.keys(), null_num_train.values())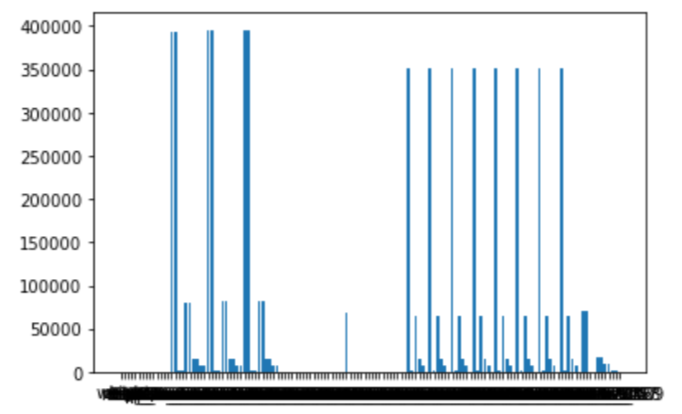
欠損値は、88個の特徴量に含まれていました。
欠損値の最大の数は395,535個で、feature_17,feature_18, feature_27, feature_28の4つで欠損値が最も多かったです。
トレーニングデータの各変数は欠損値を含めて2,390,491個あり、欠損値は各変数において多くても約16.5%でした。
テストデータの欠損値について見てみます。
同様の手順で欠損値を確認すると、テストデータにも80個の特徴量に欠損値が含まれていました(最大で1変数内に約13.5%)。
学習データ、テストデータにおいて欠損値を持つ特徴量について確認したところ同じでした。
テストデータにおいても欠損値が多いことから、欠損値の補完をどう対処するかが問題になります。
テストデータに欠損値が含まれていなければ、トレーニングデータで欠損値を含むものを削除するだけでよかったがそう簡単にはいかないようです。
欠損値の補完
欠損値がどのような条件で発生しているのか見てみます。
ある時点まではデータが取得できないために欠損値が発生している場合やデータ全体の中で点々と欠損値がある場合など考えられます。
前者であれば、ある時点までのデータをごっそり削るのも一策です。
後者の場合は、平均値や前の値で埋めるなど検討する必要があります。
欠損値が最も多かった4変数のうち、”feature_17″について欠損値の推移を見てみます。
ただし、データ量が多い為、今回は最初と最後の10%に絞りました。
# 欠損値の推移(欠損値が最も多いfeature_17)をプロットしてみる
# 欠損値:1 else:0として全体の最初から10%と最後の10%
train['feature_17'].map(lambda x:1 if x != x else 0)[:int(train.index.size*0.1)].plot()
plt.legend(loc='lower right')
plt.xlabel('0~10%')
# 90%~
train['feature_17'].map(lambda x:1 if x != x else 0)[int(train.index.size*0.9):].plot()
plt.legend(loc='lower right')
plt.xlabel('90~100%')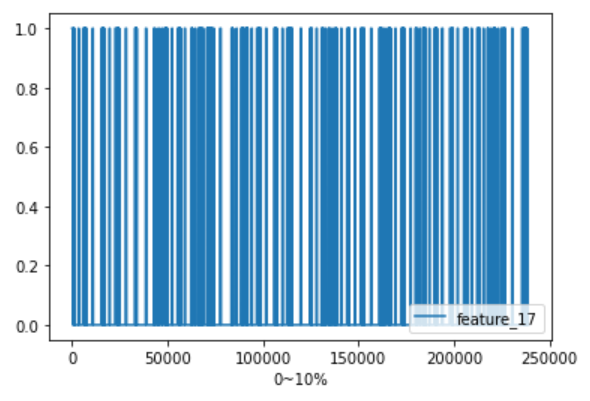
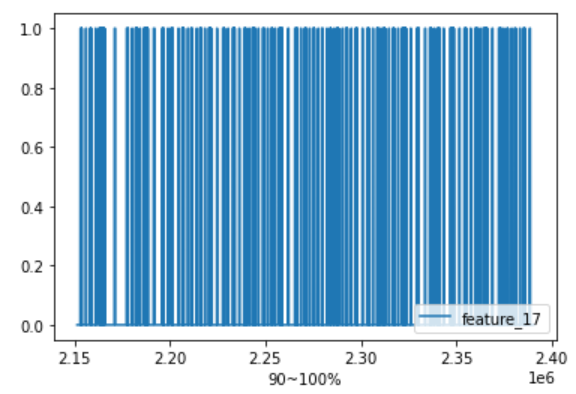
欠損値は、期間を通じてまばらのようです。
欠損値の補完方法には、単純にゼロ埋めや前後の値やその平均で補完する、全期間の平均、一定期間の平均を用いるなどいろいろあります。
今回のデータは時系列で期間幅も短いので前の値で埋め合わせをすることにします。
金融データということで、各指数の公表タイミングが異なり欠損値となってしまっている可能性もあります。ある時点のデータが欠損値の場合、そのデータは公表前であり、市場では公表前の前回の値が参照されることもあるので前の値で補完するのは自然と思えます。
train = pd.read_csv('/kaggle/input/jane-street-market-prediction/train.csv')
# 欠損値の補完(前の値で補完する)
train.fillna(method = 'ffill', inplace=True)
train.dropna(inplace=True)
# メモリ対策
train = reduce_mem_usage(train)
train.to_pickle('/kaggle/working/train_without_null.pickle')fillna()を使う際は、dfの型が同じでなければならないようです。
このままfillna()を使うと「TypeError: No matching signature found」が出てしまいます。
そのため、再度、train.csvを読み込む処理を組み込みました。
前の値で欠損値を補完しているため、欠損値でない値が出るまでは全て欠損値となっています。
補完後の各変数の欠損値の数は多くて479個であり、欠損値を含む場合は削除することにしました(つまり最初から479レコードまでは削除される)。
以上で、最低限の前処理は完了しました。
テストデータの欠損値処理は、同様に前の値で補完することにします。
したがって、テストデータにおいては最初の数レコードは評価対象外とする必要が出てきます。
データ全体について
トレーニングデータについて簡単にプロットして特徴を見てみます。
# リターンの分布と特徴
# 全部, weight=0, weight=0以外でヒストグラムをみてみる
plt.figure()
train['resp'].hist(bins=25, label='all_data', color='lightblue')
train.loc[train['weight']==0]['resp'].hist(bins=25, label='weight=0')
train.loc[train['weight']!=0]['resp'].hist(bins=25, label='weight!=0', histtype='step')
plt.legend()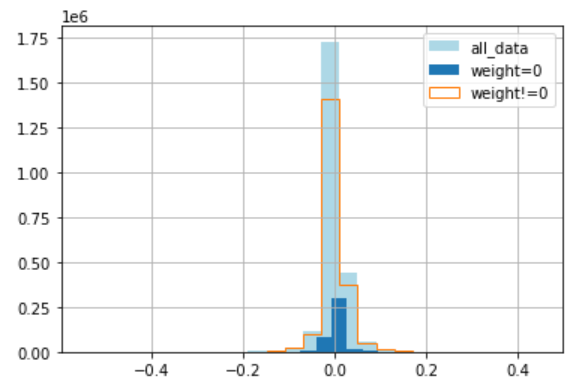
まずは、リターンの分布についてヒストグラムにしてみました。
weight=0の数が少ないことがわかります(全体の17%程度)。
weight=0はボラティリティがweight!=0に比べて小さいこともわかります。
分布の形状はweight=0はややプラスより、weight!=0はややマイナスよりとなっています。
それぞれの統計量を見てみます。
# 統計量を算出
import statsmodels.stats.api as sms
print('weight=0')
print(train.loc[train['weight']==0]['resp'].describe())
JB = sms.jarque_bera(train.loc[train['weight']==0]['resp']) # JB検定
print('歪度:{0:.4f}, 尖度:{1:.4f}'.format(JB[2], JB[3]))
print('\n weight!=0')
print(train.loc[train['weight']!=0]['resp'].describe())
JB = sms.jarque_bera(train.loc[train['weight']!=0]['resp']) # JB検定
print('歪度:{0:.4f}, 尖度:{1:.4f}'.format(JB[2], JB[3]))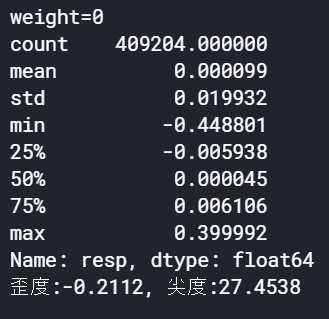
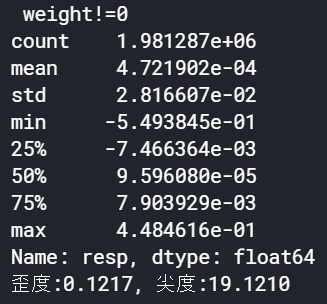
ヒストグラムを見た時とは若干結果が異なりました。
weight=0は平均は若干プラスだが、歪度はマイナス(マイナス寄り)となっています。
一方、weight!=0は平均は若干プラスで歪度はプラス(プラスより)でした。
(概観を見るだけでなくちゃんと数値化して確認することは大事だと思いました。)
weightとresp(リターン)の関係
ここまでの結果を踏まえると、weightとリターンには何かしらの特徴があるように思えます。
これらを2変数として散布図を書いてみます。
# weightとリターンの関係
plt.scatter(train['weight'], train['resp'])
plt.xlabel('weight')
plt.ylabel('resp')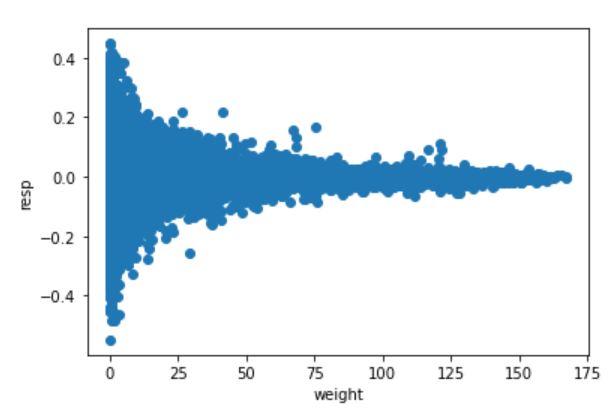
なかなか面白い散布図が描かれました。
weightが大きくなるに従い、respのばらつきは小さくなっています。
weight=0では、高いリターンは得られる可能性があるものの、同時に大きな損失を被る可能性もあります。
weightはリスク管理として機能しそうに思えます。
ただ、weightを大きくするとリターンも得られないのでその辺の調整が難しいです。
逆に、weightがある一定値より大きい場合はリターンはほぼゼロなので取引をしないという戦略を加えると良いのかもしれないです。
そうなると狙いとしては、0<weight<75くらいでresp>0の部分をうまく取り出すことになるのでしょうか?
resp(リターン)と各特徴量(feature_X)の関係
次に、respと130個の特徴量の相関を見てみるために、まずは素直にヒートマップとして表示してみます。
# 相関ヒートマップ
import seaborn as sns
sns.heatmap(train.drop(['date', 'resp_1', 'resp_2', 'resp_3', 'resp_4', 'ts_id'],axis=1).corr())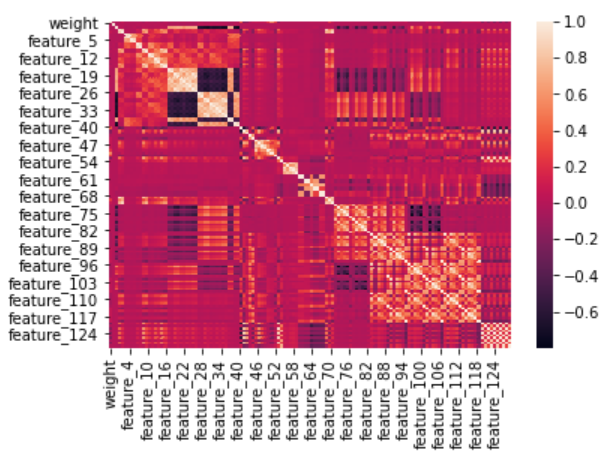
2行目がrespですが軸から表示が消えてしまっています。
すべての値を表示するには、xticklabels, yticklabelsを指定することで可能ですが、変数が多すぎるので結局読めなかったです(グラフサイズを大きくすれば可能かもしれないが…)。
2行目を大雑把に見てみると、ところどころで正・負の相関がある特徴量が見られます。
また、変数間で相関があるものがいくつも見られます。
したがって、次元圧縮してみるのもよさそうに思えます。
次元圧縮手法としては、主成分分析やオートエンコーダ、クラスタリングあたりを試したいところです。
ここで、respと相関が高い10変数を抽出してみます。
# 相関が高いものを抽出
cols = train.drop(['date', 'resp_1', 'resp_2', 'resp_3', 'resp_4', 'ts_id'],axis=1).corr().nlargest(10, 'resp')['resp'].index
cm = np.corrcoef(train[cols].values.T)
plt.subplots(figsize = (12,10))
sns.heatmap(cm, vmax=.8, linewidths=0.01, annot=True, cmap='viridis',
xticklabels=cols.values, yticklabels=cols.values, annot_kws={'size':14});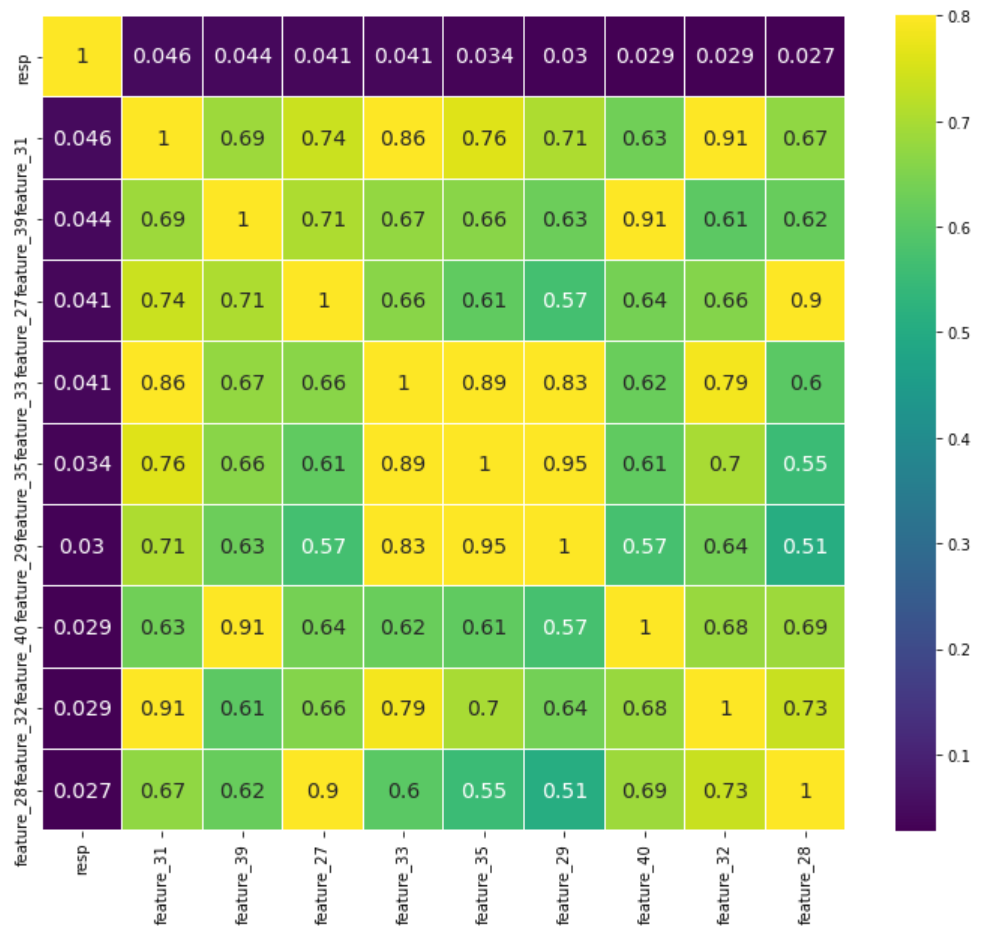
相関は高くても0.046であり、どの変数もrespとはほぼ無相関でした。
相関が低い理由としては、全期間のデータを対象としていることや外れ値の存在などが考えられます。外れ値については、最初に見ておくべきでした…。
期間を短くしたときの相関係数について見てみます。今回は、前半10%についてです。
cols = train.drop(['date', 'resp_1', 'resp_2', 'resp_3', 'resp_4', 'ts_id'],axis=1)[:int(len(train.index)*0.1)].corr().nlargest(10, 'resp')['resp'].index
cm = np.corrcoef(train[cols].values.T)
plt.subplots(figsize = (12,10))
sns.heatmap(cm, vmax=.8, linewidths=0.01, annot=True, cmap='viridis',
xticklabels=cols.values, yticklabels=cols.values, annot_kws={'size':14});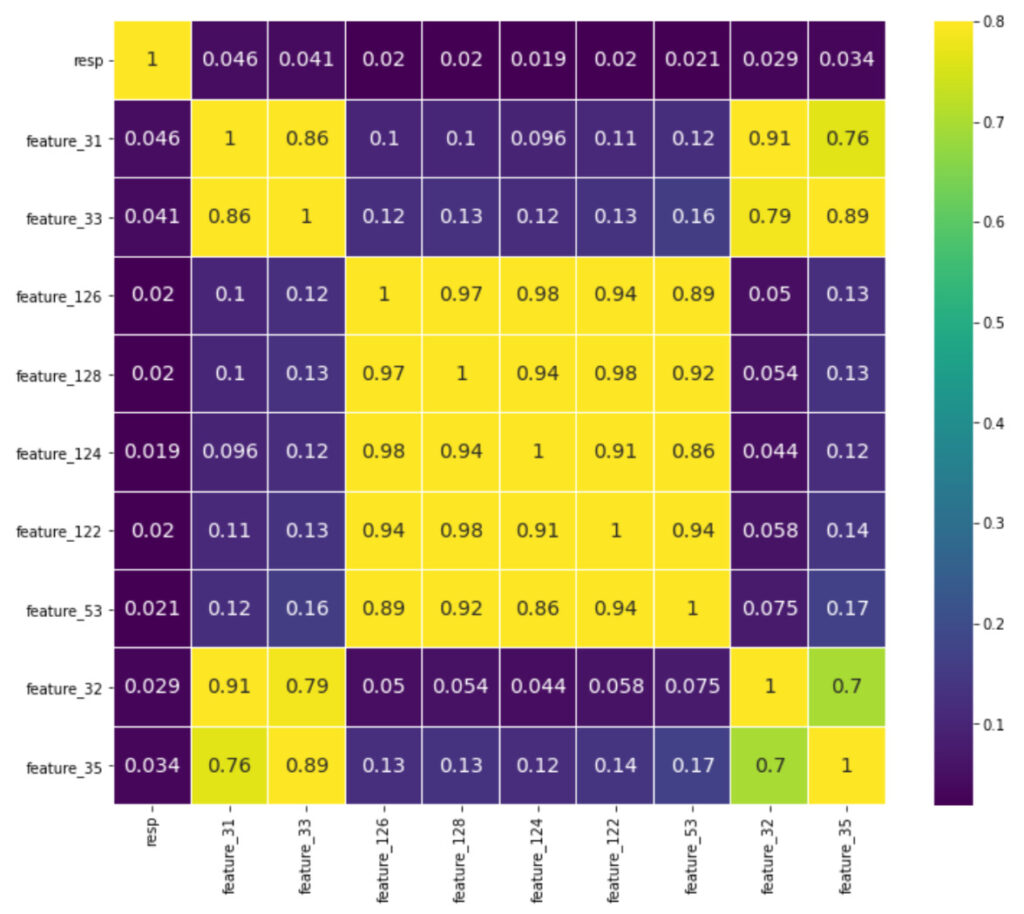
respとの相関について見てみると、抽出された変数は多少異なるものの相関係数のサイズに変化は見られなかったです。
外れ値について確認
外れ値をむやみに欠損値にしたりある値で丸めるのも適切かわからないです。
外れ値だからこそ特徴を持つということはないでしょうか。
そう考えると、外れ値処理の有無についても見ていく必要があるように思われます。
plt.figure(figsize=(20, 100))
cnt = 0
x = train.drop(['date', 'resp_1', 'resp_2', 'resp_3', 'resp_4', 'ts_id'],axis=1).copy()
for i in range(29):
for j in range(4):
plt.subplot(29, 4, cnt+1)
sns.boxplot(x=x.iloc[:, cnt])
plt.xlabel(x.columns[cnt], fontsize=10)
gc.collect() # メモリ解放
cnt += 1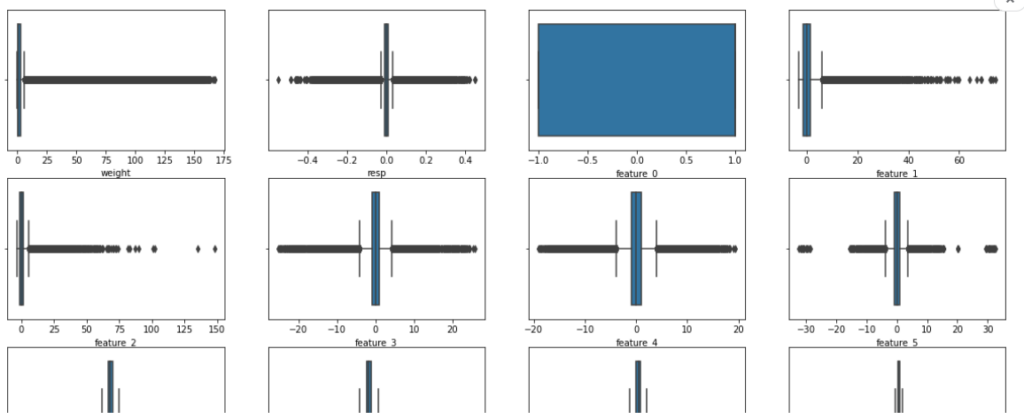
四分位に基づくと多くの変数で外れ値が散見されました。
また、全体としては左右対称かプラス方向に偏った形状をしていました。
ここで、四分位範囲に基づく外れ値判定(参考サイト)を行い、外れ値の有無がresp(リターン)に影響があるか調べてみます。
x = train.drop(['date', 'weight', 'resp_1', 'resp_2', 'resp_3', 'resp_4', 'ts_id'],axis=1).copy()
corr_outlier = []
corr_inner = []
for col_x in x.columns[1:]:
df_x = x[['resp', col_x]]
Q1 = df_x[col_x].quantile(.25)
Q3 = df_x[col_x].quantile(.75)
IQR = Q3 - Q1
th1 = Q1 - 1.5 * IQR
th2 = Q3 + 1.5 * IQR
df_outlier = df_x[(df_x[col_x] < th1) | (df_x[col_x] > th2)]
df_inner = df_x[(df_x[col_x] > th1) & (df_x[col_x] < th2)]
corr_outlier.append(df_outlier.corr().loc['resp',col_x])
corr_inner.append(df_inner.corr().loc['resp',col_x])
gc.collect()
plt.figure(figsize=(12, 10))
plt.bar(x.columns[1:], corr_outlier, color='red', label='outlier')
plt.bar(x.columns[1:], corr_inner, color='lightblue', label='inner')
plt.legend()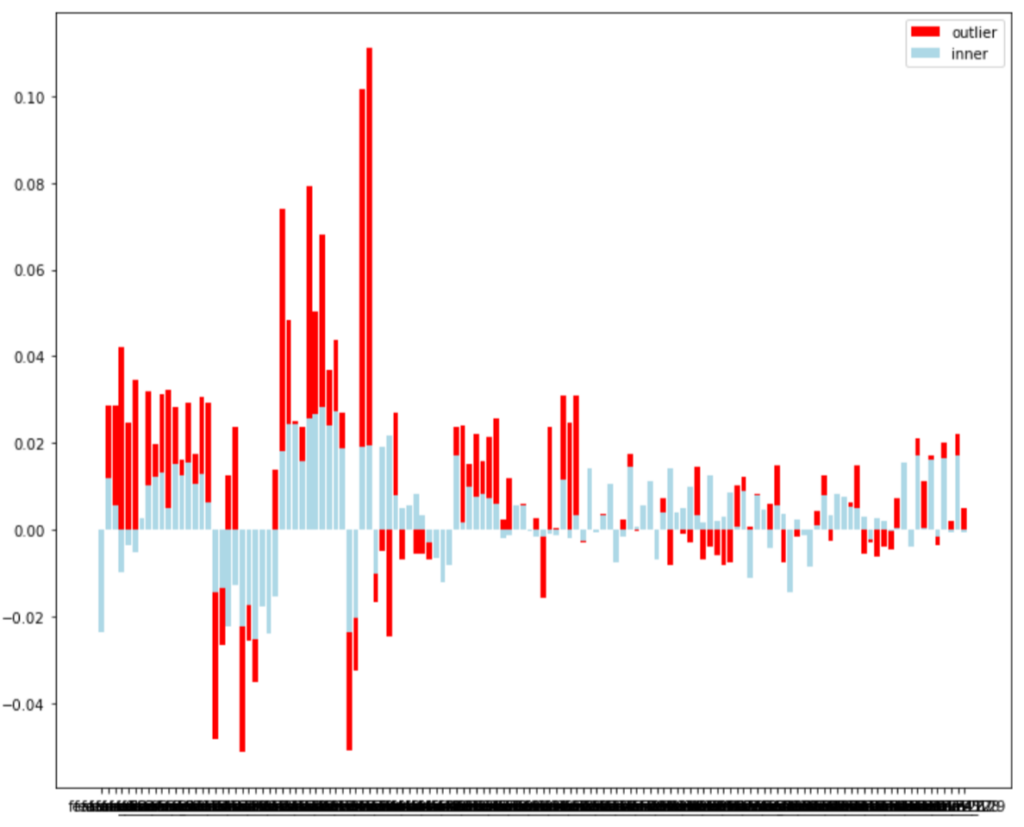
外れ値(outlier)とそれ以外(inner)についてrespとの相関係数を比較した結果が上図です。
正負の向きはほぼ等しいですが、外れ値の方が若干だが相関係数が高い傾向にあります。
この結果を見る限りでは、外れ値を丸める(除外する)のはよくないのかもしれないです。
まとめ
今回は、データ全体について大まかな特徴を見ました。
次回は、特徴量の次元を圧縮し、各クラスタごとでデータの特性を見ていきます。


コメント