プロ囲碁棋士にAlphaGo(AI)が勝利したというニュースを見た時から、同じロジックで株で勝てるAIを作れるのではないかと思った人は多くいると思う。最近になってようやく、AlphaGoのロジックである深層強化学習について学び、トレーディングAIを作ってみたので、記事にまとめておく。
結論を先に述べておくと、今回作成したAIのパフォーマンスはかなり酷いものとなっている。インデックス投資がベストという結果に…。
読者には、その点を承知の上、以降の内容を読んでもらえると幸いである。ただ、これから深層強化学習によるトレーディングAIを作成しようと考えている人には、何かしら役立つことを願っている。(プログラムは、いつか公開するかも?)
強化学習
深層強化学習を株取引に適用する前に、まずは強化学習について簡単に説明する(というよりは、自分の勉強記録として残しておく)。興味ない人は飛ばしてOK。
まず、強化学習では「環境」を与えるところから始まる。環境とは、「行動」と行動に応じた「状態」の変化が定義されており、ある状態へ到達することに対して「報酬」が与えられる空間のことである。つまり、ゲームの世界そのものである。
例えば、スーパーマリオを例にすると、「行動」とは左右の移動やジャンプが該当する。「状態」とは、マリオの位置(座標)や土管やクリボーとの距離などである。「報酬」には、「即時報酬」と「報酬の総和」がある。マリオの例だと、マリオがある時点での行動後に生存していたり、敵を倒す、クリアするというのが「即時報酬」であり、死亡やクリアしてゲームがリセットされる時点までの報酬の和が「報酬の総和」となる。
強化学習では、行動単体ではなく連続した行動で獲得できる「報酬の総和」を最大化することを目的とする。この目的を達成する為に、「環境」で「報酬」が得られる「行動」をとる必要がある。つまり、強化学習における「行動」は「報酬の総和」の最大化につながるかという観点で評価される。モデルは「行動の評価」に基づき、「行動の選び方(戦略):Policy」を学習する。
「行動の評価」とは、ある時点でとった行動が報酬の最大化にどれだけ効果があったかを評価することである。「行動の選び方」とは、ある時点における状態から最適な行動を選択することである。マリオの例に当てはめると、目の前にクリボーがいる状態を思い浮かべてほしい。
- ジャンプをしてクリボーを倒す: 1Pゲット
- 右に移動してクリボーに激突:死亡し▲100P
- 左に移動してクリボー回避:0~0.5P?(ゴールから遠ざかるのでマイナス?)
この時、実際にマリオが行った行動とその行動に対する報酬(ポイント)からその行動が将来の報酬和の最大化にどれだけ効果があったかを評価することが「行動の評価」である。この評価に基づき、「行動の選び方(Policy)」を学習することになる。また、各時点における行動は、Policyに基づき決定される。強化学習では、「行動の評価」と「行動の選択」を繰り返し学習することで、最適な戦略(Policy)を発見する。言い換えると、戦略(Policy)のパラメータを調整し、状態に応じて適切な行動を出力できるようにすることが強化学習における「学習」ともいえる。
マルコフ決定過程(Markov Decision Process)
強化学習で避けられない概念として、マルコフ決定過程(MDP)がある。強化学習では、与えられた「環境」がマルコフ性に従っていることを想定している。強化学習におけるマルコフ性とは、以下の通り。
- 遷移先の状態は直前の状態とそこでの行動のみに依存する
- 報酬は直前の状態と遷移先に依存する
このマルコフ性を持つ環境をマルコフ決定過程と呼ぶ。また、2点目の報酬のことを「即時報酬」と呼ぶ。MDPにおける「報酬の総和」は、「即時報酬(\(r\))」の合計となる。エピソードが時刻\(T\)で終わる場合、時刻\(t\)における報酬の総和\(G_t\)は以下のように定義できる。
$$G_t = r_{t+1} + r_{t+2}+\cdots+r_{t+T}$$
時刻\(t\)から先の即時報酬を合計したものとなっている。最初見たときは、将来の即時報酬を合計することに”?”を思い浮かべた。というのもの、時刻\(t\)までの即時報酬を合計するのではないかというように。私の中では、以下のような理解で腑に落ちた。
強化学習の目的に立ち返ると、『強化学習における「行動」は「報酬の総和」の最大化につながるかという観点で評価される』とあるよに、強化学習では時刻\(t\)において将来の報酬の総和をいかに最大化するかが重要である。エージェントの立場で考えると、将来の報酬の総和が最大化される行動を選択したい為、時刻\(t\)における報酬の総和は将来の即時報酬の合計となっている。
しかし、将来の即時報酬はエピソードが終了し、各時点の即時報酬が得られた時でないと正確に\(G_t\)を計算することができない。一方で、エージェントは、時刻\(t\)で将来の報酬総和を把握して、最適な行動(報酬の総和が最大になる)を選択したい。そこで、時刻\(t\)における報酬の総和は「見積もり」を立てることで対応する。見積りは不確かな値であるため、割引率\(\gamma\)を利用して以下のように定義する。
$$G_t = r_{t+1} +\gamma r_{t+2}+\gamma^2r_{t+3}\cdots+\gamma^{T-t-1}r_{t+T}$$
\(\gamma\)には0~1の値である。上式を見ると、将来になるにつれ係数である\(\gamma\)が指数的に大きくなっている(係数はかなり小さな値になる)ことから、将来の即時報酬に関する項は小さな値となる。これは、将来の不確かさを適切に表現できている。
ここで、\(G_t\)(「報酬の総和」を「見積もった」値)は期待報酬(Expected reward)または価値(Value)と呼ばれる。そして、この期待報酬(価値)を算出することを価値評価(Value approximation)と呼ぶ。
Bellman Equation
期待報酬\(G_t\)を計算する(見積もる)ためには、将来の即時報酬が必要となる。そこで、以下のように再帰的に式を変形し、\(G_{t+1}\)に適当な値を入れて計算することで、計算を持ち越すことができる。ちなみに動的計画法では、この将来の即時報酬\(G_{t+1}\)を過去の計算を使うことで計算する。これはメモ化と呼ばれている。
$$\begin{align}G_t &= r_{t+1} + \gamma(r_{t+2}+\cdots+\gamma^{T-t-2}r_T) \\
&= r_{t+1} + \gamma G_{t+1} \end{align}$$
実際は、将来の即時報酬は不明である(確率的に決まる)。そこで、期待値とすることでこの問題を対処する。エージェントは、状態\(s\)から戦略\(\pi\)に基づいて行動し、そこで得られえる価値を\(V_\pi(s)\)とすると
$$V_{\pi}(s_t) = E_{\pi}[r_{t+1}+\gamma V_{\pi}(s+t)]$$
と書ける。さらに、以下を定義する。
- 行動確率\(\pi(a|s)\):状態\(s\)で行動\(a\)をとる確率
- 遷移確率\(T(s’|s, a)\):状態\(s\)で行動\(a\)をとった時に状態\(s’\)に遷移する確率
- 報酬関数\(R(s, s’)\):状態\(s\)から状態\(s’\)に遷移した時に報酬を与える関数
これらを用いて上式を書き換える。
$$V_{\pi}(s)=\sum_{a}\pi(a|s)\sum_{s’}T(s’|s, a)(R(s, s’) + \gamma V_{\pi}(s’))$$
この式をBellman Equation(ベルマン方程式)という。
先ほどは、エージェントは「状態\(s\)から戦略\(\pi\)に基づいて行動する」としたが、「価値が最大になる行動をする」とした場合は、以下のように式を変形することができる。
$$V_{\pi}(s)= \underset{a}{max} \sum_{s’}T(s’|s, a)(R(s, s’) + \gamma V_{\pi}(s’))$$
ちなみに、戦略に基づき行動する手法をPolicyベース、価値が最大になるように行動する手法をValueベースと呼ぶ。
動的計画法における学習
動的計画法により各状態の価値を算出する方法を価値反復法(Value Iteration)と呼ぶ。価値反復法では、Bellman Equationによる価値の計算を複数回繰り返すことで値の精度を高めていく。
$$V_{i+1}(s)= \underset{a}{max} \sum_{s’}T(s’|s, a)(R(s, s’) + \gamma V_{i}(s’))$$
\(V_{i+1}\)は、前回の計算結果\(V_i\)を利用して算出される(メモ化)。そして、更新前後の差異(\(|V_{i+1}(s)-V_{i}(s)|\))が一定値より低くなった時、学習を終了する。
一方で、戦略により価値を算出し、価値を最大化するよう戦略を更新することで価値の値と戦略の精度を高めていくことを方策反復法(Policy Iteration)と呼ぶ。更新式については、価値反復法とほぼ同じであるため、割愛する。
未知の環境下における学習
ここまでは、環境情報(遷移関数と報酬関数)がわかっていることを前提に説明してきた。しかし、実際は環境情報はわからないことがほとんどである。ここからは、環境情報がわからないことを前提とする。
環境情報が未知の場合、エージェント自らが行動することで状態の遷移、報酬を調査することになる。その際、調査目的の行動と報酬目的の行動をどれだけするか決める必要がある。このバランスをとる手法にEpsilon-Greedy法がある。Epsilon-Greedy法とは、\(\epsilon\)(0.2など)の確率で探索を行い、\(1-\epsilon\)の確率で活用を行うというシンプルな手法である。
次に行動に関する修正(更新)を実績に基づき決定するか、予測(見積り)に基づき決定する必要がある。実績に基づく手法をモンテカルロ法と言い、予測に基づく手法をTD法(Temporal Difference Learning)と呼ぶ。モンテカルロ法ではエピソード終了時に獲得できた報酬の総和で修正を行うため、シンプルで正確だが、エピソード終了まで続ける必要がある(最適でない行動だったとしても…)。一方で、予測で修正を行うTD法では、エピソードの終了を待たずに修正をするため、スピード面にはメリットがあるが、正確性に欠けてしまう。
TD法を利用した学習にはいくつか種類があるが、Q-learningが代表的である。Q-learningでは、価値が最大となる状態に遷移するよう行動を決定する。つまり戦略を使用しないので、Off-Policyと呼ばれている。一方で戦略を前提とするものをOn-Policyと呼ばれている。その代表的な手法として、SARSA(State-Action-Reward-State-Action)がある。
更新式について
状態\(s\)から状態\(s’\)へ遷移し、即時報酬\(r\)が得られたとする。
エージェントは、行動前の時刻\(t\)で状態\(s\)の価値を\(V(s)\)と見積もっていたところ、実際は、\(r+\gamma V(s’)\)が得られたことになる。この見積もりと実際の報酬との差(\(r+\gamma V(s’) -V(s)\))をTD誤差(Temporal Difference Error)と呼ぶ。
したがって、更新式はこの誤差を小さくすることになるため、以下の式で価値の更新を行う。
$$V(s) \leftarrow V(s) + \alpha (r + \gamma V(s’) – V(s))$$
\(\alpha\)は学習率である。ここでは、\(t\)と\(t+1\)との差異を見たが、期間を\(t+2\)、…と増やすことも可能。そしてエピソード終了時点までの場合が、モンテカルロ法となる。
深層強化学習
深層強化学習とは、一言でいえば、強化学習にディープラーニングを使用した手法である。
強化学習では、価値評価をテーブル(Q-Table)で行っていた。テーブル管理では、連続的な状態や行動を管理しづらかったり、状態が膨大になると管理できない。この課題を解決する為に、行動価値関数にディープラーニングを使用したのが深層強化学習である。行動価値関数は、状態と行動を入力したときにその後得られる割引報酬和を出力(回帰予測)するものとなっている。
Q学習における更新は、TD誤差に対して二乗平均を利用すればよい。価値関数の更新式は、以下で表された。
$$V(s) = V(s) + \alpha (r + \gamma V(s’) – V(s))$$
Q学習の場合は、「価値が最大となる状態に遷移するよう行動を決定する」のでこれを書き換えると、(Q-learningでは、状態における行動の価値を\(Q(s, a)\)とし、慣例的にQ値と呼んでいる。)
$$Q(s, a) = Q(s, a) + \alpha (r + \gamma \underset{a}{max} Q(s’, a) – Q(s))$$
TD誤差は、
$$(r + \gamma \underset{a}{max} Q(s’, a) – Q(s))$$
であり、二乗誤差関数\(E(s, a)\)は以下のようになる。
$$E(s, a) = (r + \gamma \underset{a}{max} Q(s’, a) – Q(s))^2$$
ここで、状態\(s’\)は、状態\(s\)と行動\(a\)から求め、\(\underset{a}{max} Q(s’, a)\)はニューラルネットワークに状態\(s’\)を入力して求める。
以上のようにQ-learningに深層学習を適用した手法はDQN(Deep Q-Network)と呼ばれている。
DQNの4つの工夫点
DQNでは、学習を安定させるために以下の4つの工夫をしている。
- Experience Replay
- Fixed Target Q-Network
- 報酬のClipping
- Huber関数の利用
Experience Replay
DQNでは、各ステップの内容をメモリに保存しておき、ランダムに取り出して(replay)、ニューラルネットワークを学習させている。1ステップごとの内容をtransitionと呼ぶ。
各ステップごとに学習をすると、時間的に相関が高い内容を連続して学習してしますため、学習が安定しづらいという問題が発生する。それを回避するための手法として、Experience Replayを利用している。
Fixed Target Q-Network
行動を決定するニューラルネットワークと誤差関数の計算時に価値を求めるニューラルネットワークの2つを利用する。
Q学習のアルゴリズムでは、行動価値関数を更新するときに、\(s’\)での行動価値\(Q(s’, a)\)が必要になる。この時、更新と行動価値の算出に同じネットワークを利用すると学習が不安定になる問題が発生する。そこで、更新に必要な\(\max_a Q(s’, a)\)を算出するときは、少し前の別のQ関数を利用するこで学習を安定させている。このモデルのことをDDQN(Double-Q学習)とも言う。
報酬のClipping
各ステップで得られる報酬を-1, 0, 1のいずれかで固定させておくことで、学習を安定させる。
Huber関数の利用
Huber関数は、誤差が-1~1の間は二乗誤差になり、-1より小さいときや1より大きいときは誤差の絶対値をとる関数である。
誤差が大きい場合、二乗誤差を利用すると誤差関数の出力が大きくなりすぎて学習が安定しづらいという問題が発生する。Huber関数を利用することでこの問題を解決する工夫となる。
トレーディングAIの作成における前提
ここまで強化学習・深層強化学習について長々?と説明してきた。以降は、深層強化学習を利用してトレーディングAIを作成してみたので、それについて紹介する。
日経平均株価を対象にとレーティングAIを構築してみた。データは、pandas-datareaderを用いて、Yahooファイナンスから取得した。期間は、1965年1月1日~直近までとし、2010年12月31日までのデータを学習データとした。少なくとも10年分は検証用として利用したほうが良いと思った為、このような期間の区切り方をしている。
各時点におけるエージェントの行動ルールは以下の通り。尚、今回は手数料は考慮していない。
- ポジションをとっていない場合は、”buy”, “hold”, “sell”から行動を決定する
- ポジションをとっている場合は、”hold”(維持)か反対売買しか行動を選択できない
- ポジションをとってから5日経過した場合は、最終日の終値でポジションをクローズする
- ポジションをとってから評価損益が▲5%以上となった場合は、損切り(▲5%の損失)
各時点の状態(state)には以下のデータを利用した。
- 時点$t$における日経平均株価の対数リターン(\(R_{t}=ln(Close_{t}/Close_{t-1})\))
- 時点$t$における日経平均株価の終値における20日間ヒストリカルボラティリティ(\(HV_t\))
- 時点\(t\)における日経平均株価の終値における5日間移動平均乖離率(\(MADR5_{t}\))
- 時点\(t\)における日経平均株価の終値における20日間移動平均乖離率(\(MADR20_{t}\))
- 時点\(t\)における日経平均株価の直近14日間におけるRSI(\(RSI_{t}\))
- 時点\(t\)における評価損益(\(UnrealizedPL_{t}\))
- 時点\(t\)におけるポジション(\(Position_{t}={buy, hold, sell}\))
株価などの価格情報は期間ごとにスケールが異なる為(相場状況で価格のスケールが異なる※)為、変化率に関する情報のみにしている。
※(例)100円の変化でも基準価格が10,000円と20,000円とでは異なる。
今回は、5日以内に売買が完結するような短期トレードをイメージして、関係のありそうな変数をピックアップしてみた。また、リスク管理のような行動をとってくれたらいいなという期待を込めて、各時点での評価損益やボラティリティを含めてみた。
前日比(対数リターン)や移動平均乖離率からトレンドを判断し、ボラティリティやRSIから投資タイミングを判断するようなモデルとなることが理想である。(実際はそうはうまくいかない)
理論面との整合性について
強化学習では、最初に述べたようにマルコフ性を前提としている。
言い換えると、与えられた「環境」が一定のルールに従っていることを想定している。そのルールとは、「遷移先の状態は直前の状態とそこでの行動のみに依存する。報酬は、直前の状態と遷移先に依存する」というもの。(このルールをマルコフ性と呼び、マルコフ性を持つ環境をマルコフ決定過程(MDP)と呼んだ)
この過程を金融市場に当てはまるかは悩ましい。遷移先の状態(市場価格等)があるエージェント(個人)の行動に依存するとは到底言えない。報酬(リターン)については、直前の状態と遷移先に依存しているので問題はなさそうだが…。「エージェントの行動に基づく損益」を状態とすれば、遷移先の状態(損益)は直前の状態と行動に依存するので仮定が成立する?
強化学習を用いるのが妥当かは判断がつかないが、仮定が成立するものとしてモデル構築をすることにしている。
また、エージェントが観測できる情報(状態)は為替市場の一部に過ぎないため、本来は部分マルコフ決定過程を仮定したほうが良いみたい?(情報元)
ただ、そこまでの知見もなく、強化学習でAIトレーダーを作ってみたいという好奇心から今回はMDP(マルコフ決定過程)を前提にモデルを構築してみる。
報酬の定義
時刻\(t\)でエージェントがある行動をとった時に獲得する即時報酬は以下のように定義する。
- ポジションをとっていない時
- “buy”, “hold”, “sell”から行動を選択する。この時点では、損益が出ていない為、即時報酬は0とする。
- ポジションをとっている時(“buy” or “sell”のとき)
- ポジションをとってから4日以内の場合
反対売買を行ったときは、即時報酬は評価損益
ポジションの継続(“hold”)のときは、即時報酬は0
評価損益が▲5%となったときは、即時報酬は▲5%(損切り) - ポジションをとってから5日経過した場合
期間ルールによりポジションをクローズし、即時報酬は評価損益となる
- ポジションをとってから4日以内の場合
報酬の総和(即時報酬の和)は、学習データの最終日における総合損益とし、最大化を目指す。
記事を書いていて気付いたが、ポジションの継続の場合、即時報酬をいくらか与えるようにしたほうが良いかもしれない。というのも、売買を頻繁に繰り返すより、少ない取引回数で利益を伸ばせるに越したことはない。
ここまで記述した内容を環境として定義した。環境は、時刻\(t\)における行動\(a_t\)に対して、時刻\(t+1\)の状態\(s_t\)と即時報酬\(R_t\)を返すものとした。
ランダムエージェント
上記の環境において、行動をランダムにとるエージェントで実験してみた。ランダムと言っても、上記の条件を満たす行動の中からランダムに行動を選択するものとしている。
結果は以下の通り。
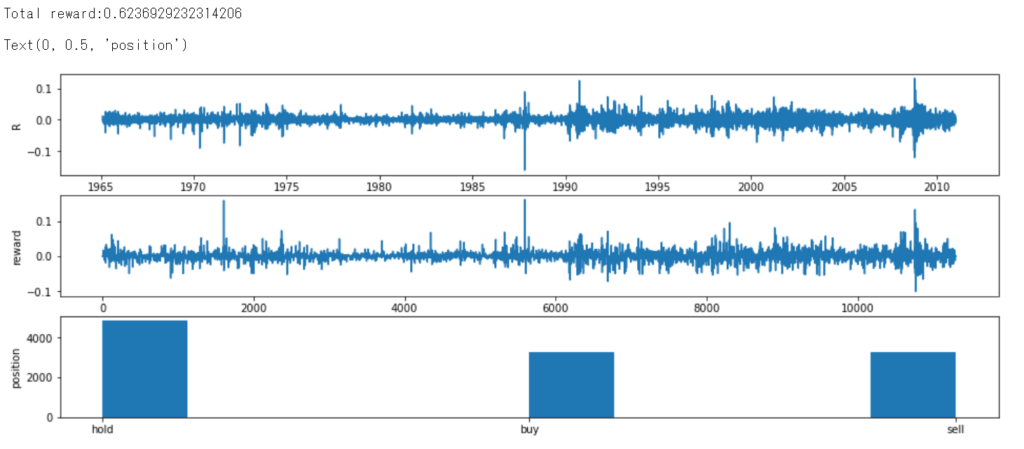
上段の図は、各時点における変化率(対数リターン)の推移を表している。中段の図は、即時報酬の推移を表している。下段の図は、学習期間における行動の棒グラフを表している。学習期間における総利益(報酬の総和)は、約62.34%となった。
ランダムに行動をしてもある一定のルールに従っているだけで利益が出ている(手数料を考慮していない点に注意)。ランダムに行動しているため、”buy”, “sell”の選択回数はほぼ等しい。また、”hold”に偏った一定のルールに従っているため、”hold”が最も選択している。
深層強化学習によるエージェント
価値関数には、以下の簡単なディープニューラルネットワークを使用した。
- 入力層:7ユニット(状態変数の数)
- 中間層:全結合層×2(32ユニット)
- 出力層:3ユニット(行動の数)
活性化関数には、ReLU関数を利用。最適化には、Adamのアルゴリズムを利用している。今回は、報酬のClippingやFixed Target Q-Networkは利用していない。Expence ReplayとHuber関数は利用している。
学習係数(\(\gamma\))を0.99として、200ステップ学習した。その時の報酬の総和の推移は以下の通り。
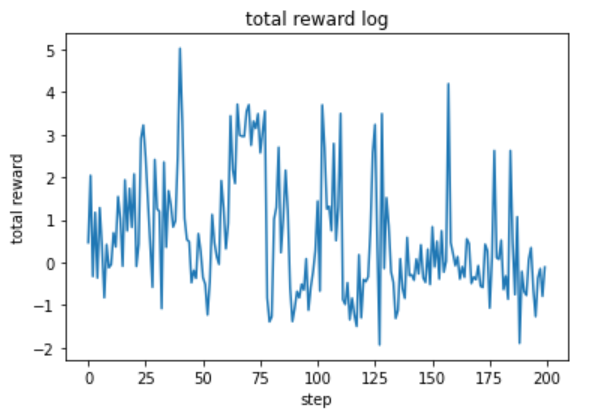
最大の報酬和は約502.13%となった。上のグラフを見ると、学習は安定しているようには見えない。ε-greedy法によりステップ数を重ねるにつれ行動のとり方は一定に収まるはずだが、今回はそのような結果にならなかった。その原因として、ステップ間における状態\(s\)が異なりすぎていた可能性が考えられる。言い換えると、ステップごとにパターンが異なりすぎていたということである。
同じようなパターンが繰り返し発生することでモデルは適切に学習し、安定したモデルとなる。今回はエージェントの行動条件をこちらである程度決めてしまったため、ステップ間の状態\(s\)が不安定になってしまった。ステップ数を増やせば安定する可能性はあるかもしれないが、他にも原因はあるように思われる。しかし、ランダムの時に比べてかなりスコアが改善された。
次にスコアが最大となった重みを用いて検証を行った。
まずは、学習データに対する結果から。検証時は、エージェントはε-greedy法により行動を決定はせず、学習した行動価値関数に基づき行動するものとする。
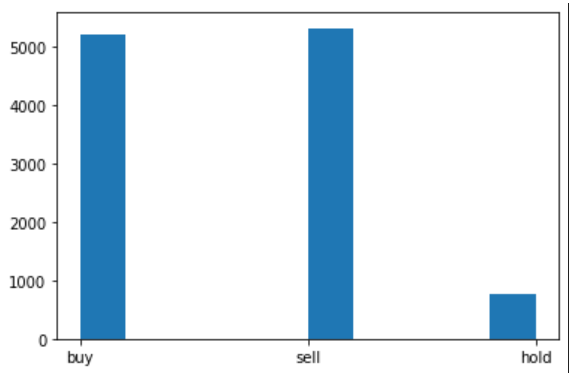
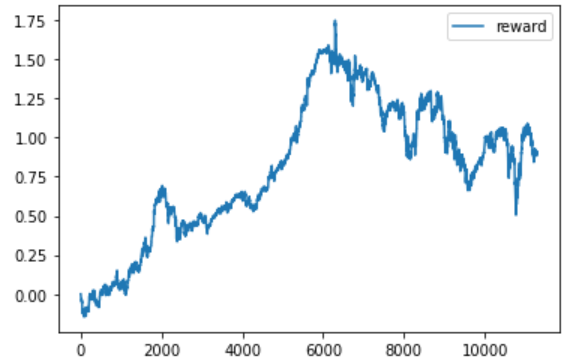
左図は、先ほどと同様に行動の回数を棒グラフで表したものである。右図は、各時点における即時報酬の総和(総利益)の推移である。
左図を見ると、ランダムの時とは対照に”buy”と”sell”に行動が偏っている。右図では、最終的な総利益は約90.45%であった。先ほどの約502.13%という利益とは大いに異なる。これは、ランダムの行動(ε-greedy)が利益に影響を与えていたことを表す。
序盤は着実に利益を伸ばしているものの、後半のパフォーマンスがかなり悪い。右のグラフを見て、すぐにお気づきの人もいたかもしれないが、日経平均株価の推移に非常に似ている。
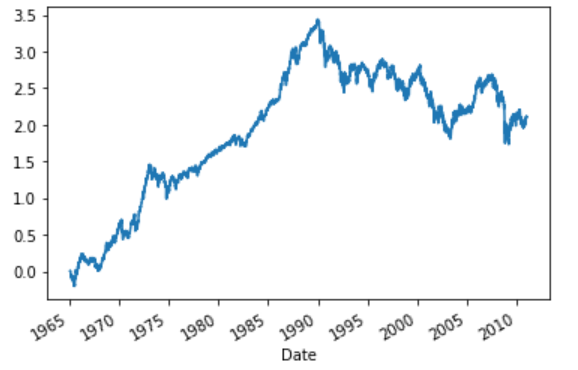
実際に日経平均株価の対数変化率の累積和の推移をグラフにしたのが上図である。ほぼ、同じような形状をしていることがわかる。実際にエージェントが取った行動のログを確認してみたところ、ほとんどが”buy”⇒”sell”を繰り返すようなものとなっていた。つまり、エージェントは日経平均株の推移に沿って売買するのが最適だと学習したことになる。(インデックス投資最強説?)
テストデータ(Out-of-sample)について見るまででもないが、結果は以下の通り。
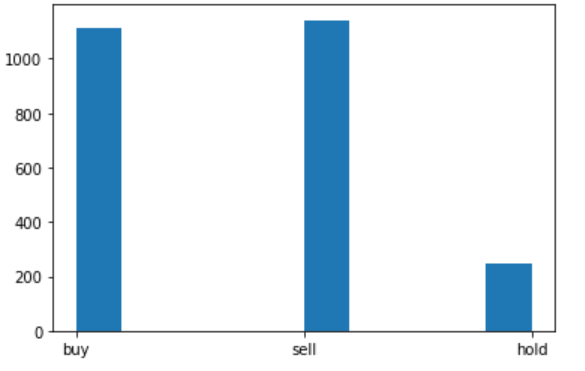
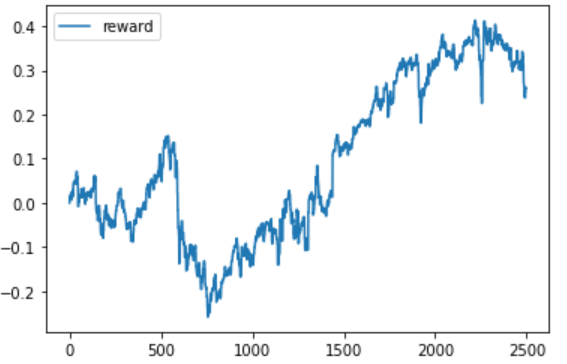
総利益は、約26.04%となった。こちらも学習データに対する結果と同様になった。
以上を踏まえると、実際に運用に用いるには到底難しい…。
モデルの改善に向けて
今回のモデル構築を改善するには、以下が必要と思われる。
(他にもあるだろうけど、とりあえず3つほど)
- 報酬の見直しと行動条件の緩和
- 状態変数の見直しと追加
- 発展形の強化学習モデルを利用する
1点目について。
今回のモデルでは、ポジションの取り方について、5日間ルールなどこちら側で決めてしまう要素が多かった。5日間ルールに従うと、エージェントはポジションをとってからクローズまで行動が限定されてしまう。各エピソードでポジションをとるタイミングは一定では無い為、エピソード間における状態変数のパターンにばらつきが生まれてしまったと思われる。この問題を回避するには、取引ルールについてもモデル側に選択の余地を残しておく必要がありそうだ。例えば、取引期間の制限を無くすことが考えられる。しかし、取引期間の制限を無くすと利益が確定するまでポジションを継続するようなモデルにもなりかねないので注意が必要である(いわゆる塩漬け状態)。
また、報酬ルールにも問題があった。今回は、ポジションをクローズしたタイミングで即時報酬を与え、ポジションを継続している間は即時報酬はゼロとしていた。このような報酬ルールだと、取引を繰り返し、即時報酬を積み上げることが最適となってしまう。本来は、取引回数が少なく、トレンドフォローで利益を伸ばすのが望ましい。したがって、ポジションの継続(“hold”)の時にも報酬を与えるなど工夫をする必要がありそうだ。(どれくらいの報酬を与えるかは要検討・・・)
2点目について。
状態変数(説明変数)には、トレーディングで一般的に用いられてそうな7つを利用した。マーケットの動きをとらえるには7つでは到底少ないと思われる。説明変数を追加することで、モデルの学習の安定性やパフォーマンスを改善することができるかもしれない。
せっかく深層学習を利用しているので、状態変数は多くしてみる価値はあると思われる。今回は、ニューラルネットワークの隠れ層の数やニューロン数を少なめに設定したのでこの辺をチューニングすれば、エージェントの行動の挙動も変わってくるのかもしれない。ただし、過学習には注意が必要である。
3点目について。
今回は、深層強化学習の基礎中の基礎であるDQNを利用した。近年では、発展形のモデル(Dueling NetworkやA2Cなど)が登場しているのでそれらのモデルに代替してあげることでモデルの学習が安定し、最適なトレーディング行動をとるようになるかもしれない。また、強化学習では初期値(乱数)の依存度が高いので、様々なシード値で試してみる必要がありそうだ。
まとめ
今回は日経平均株価に対してDQN(深層強化学習)を利用して、トレーディングAIを作ってみた。結果は、日経平均株価の値動きに沿ったような行動をするものとなってしまった。取引手数料を考慮すると明らかにマイナスである。
取引回数を抑え、インデックスの値動きに沿った行動をとるとなると、それはまさしく、パッシブ運用(インデックスファンドにおける運用)そのものである。下手な売買をするよりは、インデックス投資をするのが良いのかもしれない。
インデックス投資で着実に資産を構築していくのが健全なのかもしれない。しかし、それでは面白くない(ロマンが無い)ので、インデックス投資は確定拠出年金で行うこととして、引き続き、シストレの開発に励みたいと思う。
今回のモデルをベンチマークとして、深層強化学習モデルの改良や他の深層学習モデルをいろいろ試していきたい。
参考にした書籍
・機械学習スタートアップシリーズ Pythonで学ぶ強化学習 [改訂第2版] 入門から実践まで (KS情報科学専門書)
実装に加え、理論面の説明も書学者向きで分かりやすかった。ただ、プログラムのコードについては説明がなく、開発経験が多少ある人に向ている印象。個人的には、プログラムは少しわかりづらかった。
・つくりながら学ぶ!深層強化学習 PyTorchによる実践プログラミング
理論よりは実装した人向け。まず実装してみたいという人には良いかも。今回のトレーダーAI作成もかなり参考にしている。DQNに限らず、発展形のモデルについての実装も丁寧で、すぐに実装に移せそうである。


コメント