前回の記事に続き、今回も「Python3ではじめるシステムトレード ──環境構築と売買戦略」で学んだことを整理します。
前回は、日経平均株価のデータをヒストグラムを用いて視覚的に分析しました。
今回は、他の視覚化方法を用いて日経平均株価を分析していきます。
散布図
前回と同様に、時系列の\(j\)日間隔の変化率\(P_t/P_{t-j}-1\)を算出し、それをその\(j\)日間前の変化率\(P_t/P_{t-2j}-1\)と比べてみます。
ここで、\(j\)は移動する日数であり、変化率の自己相関を散布図で表現しているのことに近いです。
自己相関が無ければ、散布図は綺麗な円形になるはずです。
1日間隔の変化率
まずは、日経平均株価の1日間隔の変化率について散布図を書いてみます。
\(x\)軸が\(t-1\)日の変化率、\(y\)軸が\(t\)日の変化率です。
散布図の右側には、標本自己相関のコレログラムを書いています。
import statsmodels.api as sm
fig = plt.figure(figsize=(8, 4))
# 散布図
ax1 = plt.subplot(1, 2, 1)
plt.scatter(chg_N225, chg_N225.shift(1), color='gray', alpha=0.05) # 散布図を描写
plt.xticks([-0.2, 0, 0.2]) # x軸のメモリ
plt.title('1 days')
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')
plt.hlines([0], -0.1, 0.1) # 平行線を描写
plt.vlines([0], -0.1, 0.1) # 垂直線を描写
# 標本自己相関のコレログラム
ax2 = plt.subplot(1, 2, 2)
fig = sm.graphics.tsa.plot_acf(chg_N225.squeeze(), lags=5, ax=ax2, color='gray')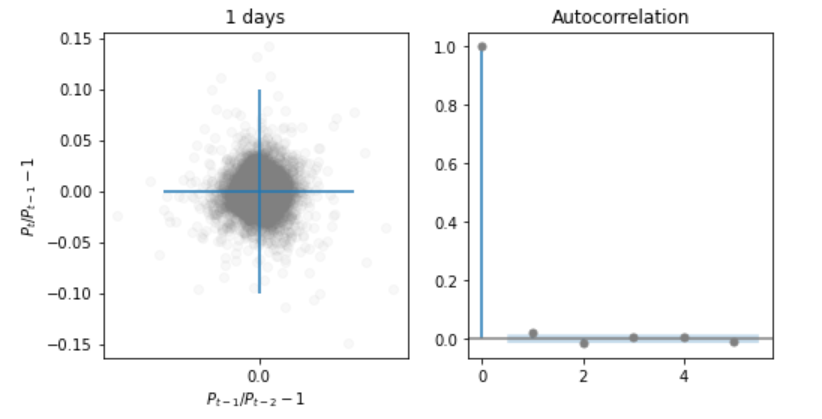
散布図を見みると、全体として完全な円形ではなく、若干のひずみが見られます。中央部分は、ひし形に近いです。
これは、変化率が大きな日の次の日には小さな変化率の日が生じやすい現象を表しています。
同様に、変化率の小さな日の次の日には大きな変化率の日が来ることを表しています。
右側のコレログラムからは、自己相関がみられませんでした。
以上のように、散布図からコレログラムでは得られない情報を見ることができます。
250日間隔の変化率
次に前回同様に、250日間隔の変化率\(P_t/P_{t-250}-1\)についてみてみます。
比較対象は、\(P_{t-250}/P_{t-500}-1\)とします。
これは、変化率の算出に用いるデータに重複が無いようにするためです。
# 250日変化率
chg250_N225 = N225.pct_change(250).dropna()
fig = plt.figure(figsize=(8, 4))
# 散布図
ax1 = plt.subplot(1, 2, 1)
plt.scatter(chg250_N225, chg250_N225.shift(250), color='violet', alpha=0.05) # 散布図を描写
plt.title('250 days')
plt.xlabel('$P_{t-250}/P_{t-500}-1$')
plt.ylabel('$P_{t}/P_{t-250}-1$')
plt.hlines([0], -0.8, 1) # 平行線を描写
plt.vlines([0], -0.8, 2) # 垂直線を描写
# 標本自己相関のコレログラム
ax2 = plt.subplot(1, 2, 2)
fig = sm.graphics.tsa.plot_acf(chg250_N225.squeeze(), lags=500, ax=ax2, color='gray')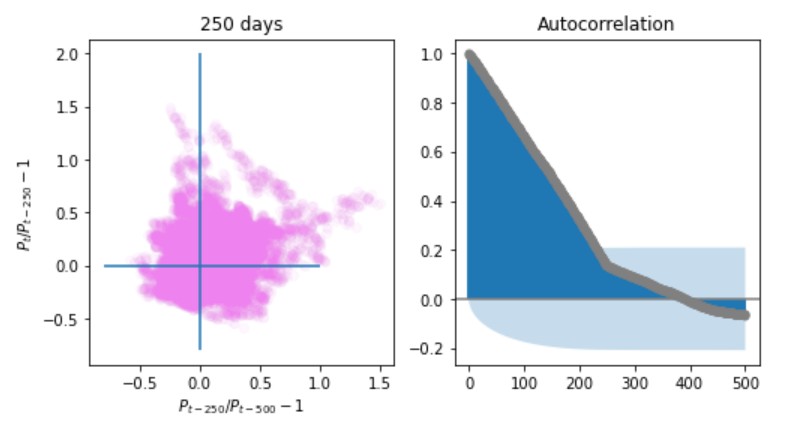
散布図から大きな変化率の後には小さな変化率の期間が表れてるという現象が更に強調されています。
散布図から以下が読み取れます。
- 250日間で価格が動かなかったら、次の250日間では価格は-50%~+150%まで動く可能性がある
- 250日間で50%で下落した後には次の250日間で50%下落・上昇する可能性が無い
- 250日間で50%上昇した後は、次の250日間で-50%~100%の可能性がある
この散布図から特徴を結論付けるのは困難だが、様々な特徴を見ることができました。
コレログラムでは、250日の変化率が1日ごとに移動していくので、250日までは重複したデータを用いています。
250日付近からは自己相関自己相関がゼロである可能性が見られます。つまり、コレログラムによると、重複のない250日間隔の変化率には自己相関がないということになります。
散布図では、コレログラムでは見ることができない相関について読み取ることができました。
バブル崩壊前後の変化率
これまでの記事で見てきたように、バブル崩壊前と後で価格の動きのメカニズムに変化があるのであれば、散布図の分析でも違いが出るはずです。
まずは、1日間隔の散布図を書いてみます。
fig = plt.figure(figsize=(8, 4))
# 散布図( バブル崩壊前)
before = chg_N225[:'1989/12/31']
ax1 = plt.subplot(1, 2, 1)
plt.scatter(before, before.shift(1), color='gray', alpha=0.05)
plt.title('before bubble crush')
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')
plt.hlines([0], -0.1, 0.1) # 平行線を描写
plt.vlines([0], -0.1, 0.1) # 垂直線を描写
# 散布図( バブル崩壊語)
after = chg_N225['1989/12/31':] # バブル崩壊後
ax2 = plt.subplot(1, 2, 2)
plt.scatter(after, after.shift(1), color='gray', alpha=0.05)
plt.title('after bubble crush')
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')
plt.hlines([0], -0.1, 0.1) # 平行線を描写
plt.vlines([0], -0.1, 0.1) # 垂直線を描写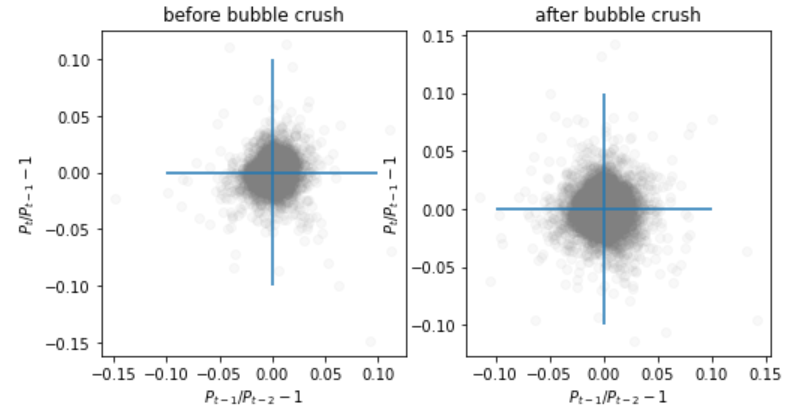
左側がバブル崩壊前で、右側がバブル崩壊後です。
バブル崩壊後は、価格の変動が大きくなっており、その影響で円が大きくなっています。
また、バブル崩壊前の分布の形状についてみてみると、やや右に偏っており、正のフィードバックがかかっているように思われます。
次に250日間隔の変化率を見てみます。
fig = plt.figure(figsize=(8, 4))
# 散布図( バブル崩壊前)
before = chg250_N225[:'1989/12/31']
ax1 = plt.subplot(1, 2, 1)
plt.scatter(before, before.shift(250), color='gray', alpha=0.05)
plt.title('before bubble crush')
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')
plt.hlines([0], -0.8, 1.8) # 平行線を描写
plt.vlines([0], -0.8, 2) # 垂直線を描写
# 散布図( バブル崩壊語)
after = chg250_N225['1989/12/31':] # バブル崩壊後
ax2 = plt.subplot(1, 2, 2)
plt.scatter(after, after.shift(250), color='gray', alpha=0.05)
plt.title('after bubble crush')
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')
plt.hlines([0], -0.8, 1.8) # 平行線を描写
plt.vlines([0], -0.8, 2) # 垂直線を描写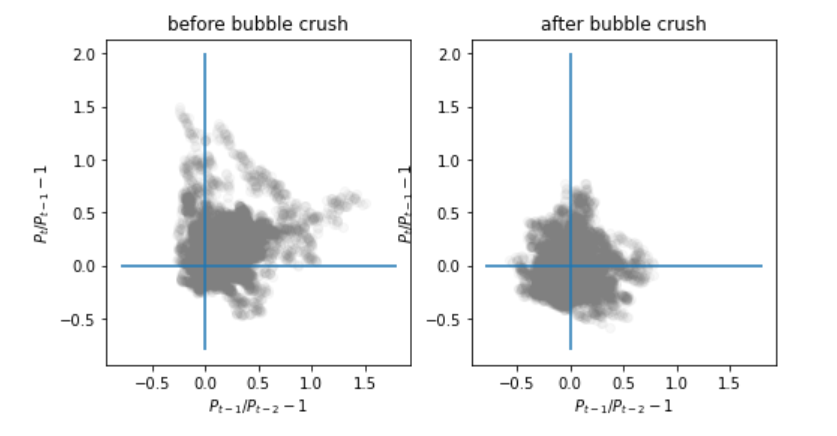
250日間隔では、先ほどとは異なった印象を受けます。
バブル前では、上昇トレンドであったこともあり、プラス方向に偏っています。
一方、バブル崩壊後は、穏やかな価格の動きの後には、上昇トレンドや下降トレンドが発生している可能性が見られます。
また、バブル崩壊後では、250日間隔の価格変化が比較的小さいことがわかります。
1日間隔の変化率では、バブル崩壊後の方が価格の変化が大きかったですが、250日間隔の変化率では対照的な結果となりました。
チャート(変化率の最大と最小値)
価格変化率の対象を1日~250日として、それぞれの価格の推移について特徴を見てみます。
異なる期間の一連の変化率の特性を、最大値、最小値、平均値により表現してみます。
時間の経過とともに価格が動ける範囲は広がるため、大きく上昇・下落することができます。
plt.figure()
high = []
low = []
ave = []
for i in range(250):
change = N225.pct_change(i)
high.append(change.max())
low.append(change.min())
ave.append(change.mean())
plt.plot(high, label='high', linestyle='--')
plt.plot(low, label='low', linestyle='--')
plt.plot(ave, label='ave', linestyle='--')
plt.legend(loc='upper left')
plt.title('all data')
plt.xlabel('$t$')
plt.ylabel('$P_{t}/P_{t-1}-1$')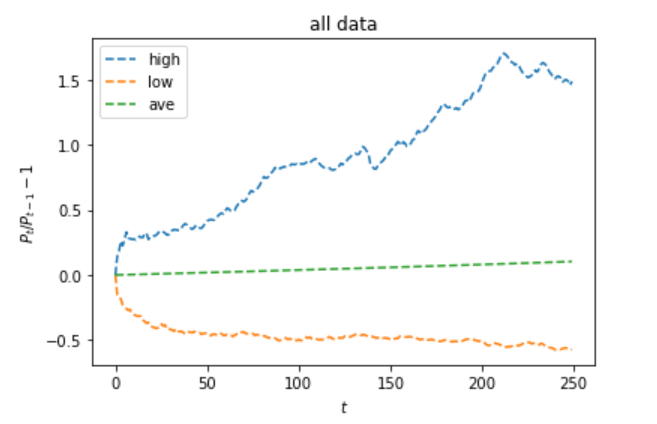
理論的に価格がランダムウォークに従えば、時間の経過に比例して価格の動ける範囲は広がるはずです。
価格が下落する際は、lowに着目してみると、その様子が見られる。
しかし、上昇に関してhighに着目してみると、広がる時期と停滞する時期に分かれているように見えます。
次に、バブル崩壊前の様子を見てみます。
plt.figure()
high = []
low = []
ave = []
for i in range(250):
change = N225[:'1989/12/31'].pct_change(i)
high.append(change.max())
low.append(change.min())
ave.append(change.mean())
plt.plot(high, label='high', linestyle='--')
plt.plot(low, label='low', linestyle='--')
plt.plot(ave, label='ave', linestyle='--')
plt.legend(loc='upper left')
plt.title('before buble crush')
plt.xlabel('$t$')
plt.ylabel('$P_{t}/P_{t-1}-1$')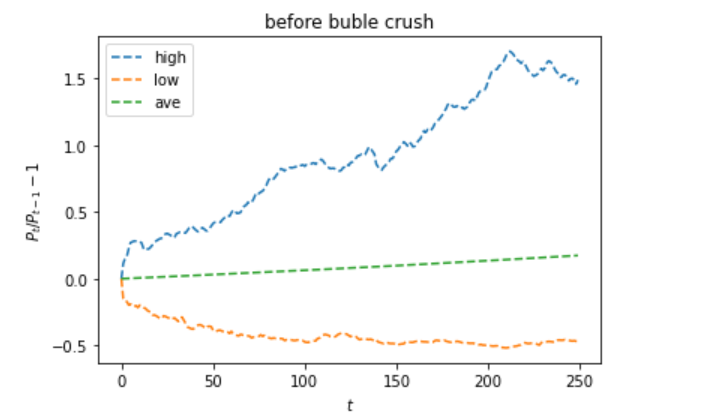
最大値のグラフについては、先ほどとほぼ同じ形状が描かれました。
つまり、先ほどのグラフは、バブル崩壊前の特性を強く反映していたものとなっていたことがわかります。
下落に関しては、バブル崩壊後の影響を受けていそうです。
そこで、次にバブル崩壊後について同様のグラフを書いてみます
plt.figure()
high = []
low = []
ave = []
for i in range(250):
change = N225['1989/12/31':].pct_change(i)
high.append(change.max())
low.append(change.min())
ave.append(change.mean())
plt.plot(high, label='high', linestyle='--')
plt.plot(low, label='low', linestyle='--')
plt.plot(ave, label='ave', linestyle='--')
plt.legend(loc='upper left')
plt.title('after buble crush')
plt.xlabel('$t$')
plt.ylabel('$P_{t}/P_{t-1}-1$')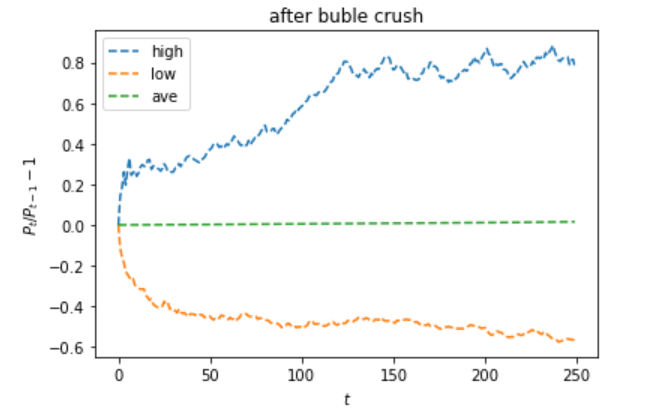
バブル崩壊後では、最小値の下落は急激に起こり、最大値の上昇は半年間かけておこるが、それ以降は停滞してしまうことがわかります。
平均はほぼ一直線となりました。
まとめ
今回は、散布図やチャートを用いて日経平均株価の変化率の特徴を分析しました。
主に以下が確認できました。
- 散布図ではコレログラムでは見ることのできない特徴を捉えることができた
- 最大値・最小値によるチャートでは、価格変化の期間構造についてみることができた
- 前回のヒストグラムによる分析を含めて、変化率の期間幅を変えることで異なった特徴を見ることができた
金融データの特徴を2回の記事に分けて分析しましたが、グラフを描写し、データの構造・特性を把握することが重要です。本記事が少しでもお役に立てれば幸いです。



コメント