本記事は「確率的トレンド」や「ランダムウォーク」について、「Python3ではじめるシステムトレード ──環境構築と売買戦略」で学んだことやそれに関して調べたことを整理します。
確率的トレンドとは
一言でまとめると、乱数の和から発生したトレンドを確率的トレンドです。
また、そのような動きはランダムウォークの特徴の一つとされています。
金融商品の価格は、ランダムウォークとしてモデル化されることがよくあります。
価格がランダムである理由としては、金融市場の効率性を反映した結果であるなど様々諸説があります。
まずは、その様子をシミュレーションで確認してみます。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 1000個の乱数を作成
randoms = np.random.randint(low=-1, high=2, size=1000)
x = range(len(randoms))
# グラフを各
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.plot(x, randoms.cumsum())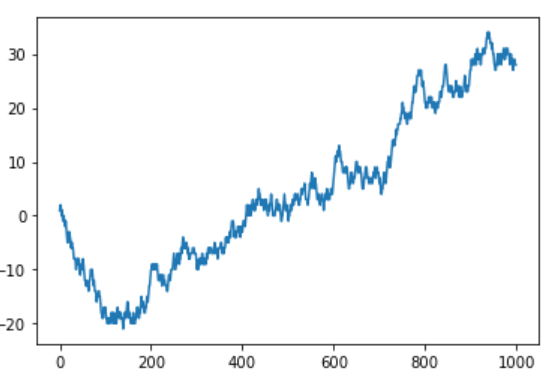
10回に1回くらいは、上昇トレンドや下降トレンドのような形状をしたものが得られました。
確率過程とは
ランダムに発生した変数を時間の順に並べたものを確率過程といます。
時系列データを扱う場合は、得られたデータを標本と呼ばず、実現値と呼びます。
その理由は、特定の確率過程から抽出され、実現した特別な一連の値だからです。
金融関連の価格は、とびとびの値をとるため、離散型の確率変数となります。
また、金融市場では取引時間は連続では無い為、離散時間の確率過程となります。
一方で、価格の理論を構築するような場合は、連続時間の確率過程を使うと便利であり、ブラン運動やウィーナー過程といった連続時間の確率過程が利用されます。(この辺が参考になりそう)
これらの確率過程は、定常な確率過程と非定常な確率過程に分けることができます。
定常確率過程とは、確率変数の値が初期値から大きく離れることはなく、その周辺をうろうろする状態を継続することができる確率過程のことです。
その際に、確率変数の平均、分散、共分散は時間に対して一定となります。
非定常確率過程とは、時間の経過とともに、確率変数の平均、分散、共分散などが変化する確率過程のことです。
確定的トレンドは非定常過程の一例です。確率過程から確定的トレンドを取り除くと、残った確率過程は定常過程となります。そのため、確定的トレンドはトレンド定常性とも呼ばれています。
ランダムウォーク
資産価格の分散が時間の経過とともに変化するのであれば、その確率過程はランダムウォークとしてモデル化できるます。
ドリフト無しランダムウォーク
\(t\)時の金融資産価格を\(W_t\)とすると、
$$W_t = W_0 + \sum^{t}_{i=1} w_i$$
となります。ここで\(w_i\)は平均ゼロ、分散\(\sigma^2\)の正規分布に従う確率変数であり、攪乱項とも呼ばれます。
このモデルは、以下のように書き換えることもできます。
$$W_t = W_{t-1} + w_t$$
ここで、(\w_t\)の期待値はゼロ(\E(w_t)=0\)です。
したがって、以下が成立します。
$$var(w_t) = E(w_t^2) – (E(w_t))^2 = E(w_t^2) = \sigma^2$$
よって、\(W_t\)の平均と分散は
$$E(W_t) = W_0$$
$$var(W_t) = var(W_{t-1} + w_t) = t \cdot \sigma^2$$
となります。期待値は定数だが、分散は時間の関数になっていることがわかります。
ドリフト付きモデル
ドリフト無しランダムウォークモデルに切片を加えたモデルがドリフト付きモデルです。
$$W_t = \alpha + W_{t-1} + w_t$$
ここで、\(\alpha\)は定数であり、ドリフト率と呼ばれます。このモデルの特性は、
$$W_t = \alpha \cdot t + W_0 + \sum^{t}_{i=1}w_i$$
で表されます。ドリフト項がトレンドの役割を担っています。
\(W_t\)の期待値と分散は、
$$E(W_t) = W_0 + \alpha \cdot t$$
$$var(W_t) = t \cdot var(w_t) = t \cdot \sigma^2$$
どちらも時間の関数となります。また、\(W\)の差分の期待値は、
$$\begin{align} E(W_t – W_{t-1}) &= E(W_t) – E(W_{t-1}),\\
&= E(W_t) – {E(W_t-\alpha-w_t)}\\
&=E(\alpha) + E(w_t) = \alpha \end{align}$$
となります。
見せかけの確率的トレンド
現在の価格の動きは独立です。
したがって、上昇と下落を繰り返しながら、上昇トレンドと下降トレンドの発生が可能となります。
このトレンドは、ランダムな現象の結果であるため、この価格の動きから売買タイミングを測り利益を上げることはできないです。
しかし、この確率的トレンドを最小二乗法で線形回帰を行うとき、確率的トレンドと判断されてしまうことがあり、これを”見せかけの確定的トレンド”と言います。
ランダムウォークの判定
ランダムウォークであるかどうかの判定問題を単位根問題と言います。
定常過程においては、母集団から抽出された標本は、数が増えれば標本平均は真の平均に近づき、この差が従う分布は標本の増加に従い正規分布に従うという中心極限定理が成立します。
しかし、単位根を持つ非定常な過程では、この中心極限定理が成り立たず、問題となります。
単位根
金融資産の価格(\(W\))を線形回帰式
$$W_t = \kappa W_{t-1} + w_t$$
で表し、\(\kappa=1\)であるならば、このモデルは単位根を持つと言います。
(つまり、ドリフト無しランダムウォークモデルが成り立つということ?)
単位根を持つとその時系列は、非定常確率過程になり、分散は時間の経過とともに発散します。
このような非定常確率過程では、最小二乗法は使えないです。
したがって、もし1次の階差
$$\Delta W_t = W_t – W_{t-1} = (\kappa-1)W_{t-1} + w_t = \gamma W_{t-1} + w_t$$
をとって、\(\gamma=0\)であれば、上式は\(W_t=W_{t-1} + w_t\)となり、\(W_t\)がランダムウォークモデルである可能性があります。
したがって、帰無仮説を\(\gamma=0\)として仮説検定を行えばよいです。
この帰無仮説を棄却できなければ、時系列はランダムウォークである可能性があります。
このような検定の仕方をディッキー・フラー検定(DF検定)と言います。
拡張ディッキー・フラー検定(ADF検定)
ADF検定はDF検定を次のように拡張したものです。
$$\Delta W_t = \alpha + \beta \cdot t + \gamma W_{t-1} + \sum^{t}_{i=1}\sigma_i W_{t-1} + w_t$$
\(\alpha\)、\(\beta\)、\(\sigma\)をゼロとすれば、DF検定となります。
statsmodelでは以下について検定が行えます。
- \(\Delta W_t = \gamma W_{t-1} + \sum^{t}_{i=1}\sigma_i W_{t-1} + w_t\)
- \(\Delta W_t = \alpha + \gamma W_{t-1} + \sum^{t}_{i=1}\sigma_i W_{t-1} + w_t\)
- \(\Delta W_t = \alpha + \beta \cdot t + \gamma W_{t-1} + \sum^{t}_{i=1}\sigma_i W_{t-1} + w_t\)
- \(\Delta W_t = \alpha + \beta \cdot t + \eta \cdot t^2+ \gamma W_{t-1} + \sum^{t}_{i=1}\sigma_i W_{t-1} + w_t\)
検定結果として、帰無仮説を棄却できなければ、データはランダムウォークと判定されます。
まとめ
本記事ではランダムウォークについて理論面から簡単にまとめました。
次回は、実際に日経平均株のデータについてランダムウォークの検証を行います。



コメント