金融データの視覚化の基本と分析①

本記事では「Python3ではじめるシステムトレード ──環境構築と売買戦略」で学んだことや調べたことを整理します。

今回は日経平均株価のデータを視覚化し、簡単な分析してみました。
視覚的にデータの概要を掴むことは、データ分析で大切なプロセスです。
金融データを分析する際に本記事が少しでもお役に立てたら幸いです。

ヒストグラム
まとめ

ヒストグラム

まず最初にヒストグラムを用いて分析してみます。

これまで、前日との変化率\(P_t/P_{t-1}-1\)を中心に分析してきましたが、今回は、\(P_t/P_{t-j}-1\)のjの値を変化させてその特徴を見てみます。

１日間隔の変化率(\(j=1)\)

日経平均株価の１日間隔の変化率\(P_t/P_{t-1}-1\)を1949年から直近までのデータを用いてヒストグラムを書いてみます。

import pandas as pd
import pandas_datareader.data as pdr
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 日経平均株価のデータを取得
N225 = pdr.DataReader('NIKKEI225', 'fred', '1949/5/16').dropna()
chg_N225 = N225.pct_change().dropna() # 変化率
# ヒストグラムを書く
plt.figure()
ax = plt.subplot(1, 1, 1)
chg_N225.hist(bins=100, ax=ax)
plt.xlabel('$P_{t}/P_{t-1}-1$')
plt.ylabel('frequency')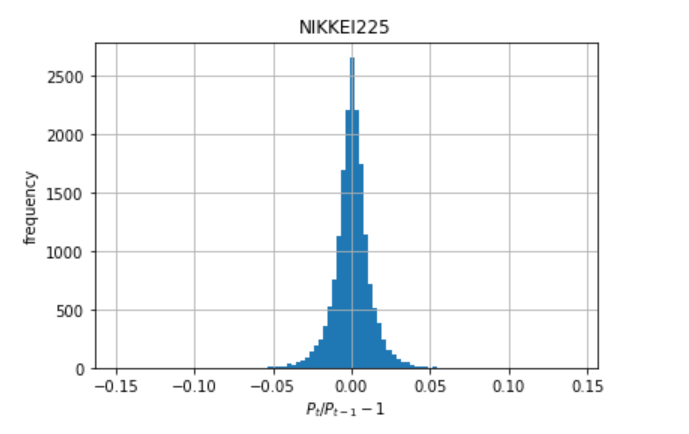

更に日経平均株価の変化率の平均と分散を用いて、正規分布を重ねて書いてみる。

from scipy.stats import norm
fig = plt.figure()
ax = plt.subplot(1, 1, 1)
x = np.linspace(chg_N225.min(), chg_N225.max(), 100)
pdf = norm.pdf(x, chg_N225.mean(), chg_N225.std())
chg_N225.hist(bins=100, density=True, ax=ax) # dennsity=True:確率密度関数
plt.plot(x, pdf)
plt.xlabel('$P_{t}/P_{t-1}-1$')
plt.ylabel('probability density function')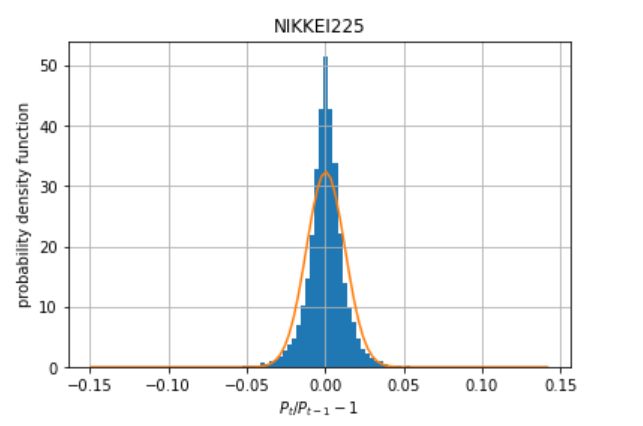

上図を正規分布と比較すると以下の特徴があります。

中央付近の尖りが強い

中間部分が薄い
すそ野の部分が厚い

分布の形状を表現する尺度として、歪度（わいど）と尖度（せんど）があります。

歪度とは

分布のひずみを表す尺度で、歪度がゼロであれば左右対称の分布となります。
正の歪度とは、分布の山が左側に寄っていて、右側にゆっくりとすそ野が伸びていくようなもので。す。負の歪度とは、分布の山が右側に寄っていて、左側のすそ野がゆっくりと伸びていくようなものです。

金融関連の価格の時系列は正の歪度をもつことが多いです。

尖度

分布のすそ野の厚さ、または中央の山のとがり具合を表します。
正規分布の尖度は３です。尖度が大きければ、すそ野は広がります。

先ほどの分布の尖度と歪度を求めてみると、以下のおとりになる。

# 尖度と歪度の算出
skew = chg_N225.skew()[0] # 歪度
kurt = chg_N225.kurt()[0] # 尖度
print('歪度:{0:.4f}, 尖度:{1:.4f}'.format(skew, kurt))

歪度:-0.1311, 尖度:9.3976

この値を見ると、上記の分布に歪みはほとんどなくすそのが厚いことがわかります。

250日間隔の変化率(\(j=250)\)

次に、250日間隔の変化率\(P_t/P_{t-250}-1\)で上記と同様に分布の特徴を見てみます。

chg250_N225 = N225.pct_change(250).dropna() # 250日変化率
# ヒストグラムを書く
plt.figure()
ax = plt.subplot(1, 1, 1)
chg250_N225.hist(bins=100, density=True, ax=ax)
# 正規分布を重ねて書く
x = np.linspace(chg250_N225.min(), chg250_N225.max(), 100)
pdf = norm.pdf(x, chg250_N225.mean(), chg250_N225.std())
plt.plot(x, pdf)
plt.xlabel('$P_{t}/P_{t-250}-1$')
plt.ylabel('frequency')
# 尖度と歪度の算出
skew = chg250_N225.skew()[0] # 歪度
kurt = chg250_N225.kurt()[0] # 尖度
print('歪度:{0:.4f}, 尖度:{1:.4f}'.format(skew, kurt))

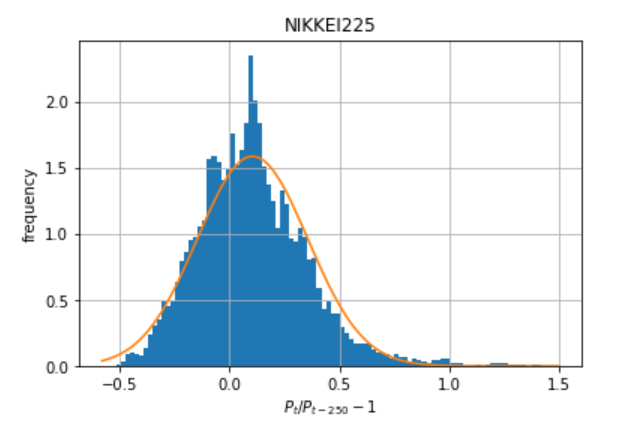
歪度:0.8171, 尖度:1.9550

上図を見てみると、ほぼ正規分布に見えます。
歪度と尖度から、分布の歪みはゼロに近く、尖度は先ほどよりもかなり小さくなっており、正規分布に近づいている様子が見られます。

バブル崩壊前と崩壊後の比較

バブル崩壊前と崩壊後で経済の背後にある構造が変化しているのであれば、どこかに明確な変化が見て取れるはずです。
そこで、バブル崩壊前と崩壊後についてグラフを書き、比較してみます。

まずは、1日間隔の変化率から確認します。

# バブル崩壊前
before = chg_N225[:'1989/12/31']
plt.figure()
ax1 = plt.subplot(1, 2, 1)
before.hist(bins=100, density=True, ax=ax1)
plt.title('before buble crushed')
plt.xlabel('$P_{t}/P_{t-1}-1$')
plt.ylabel('probability density function')
# バブル崩壊後
after = chg_N225['1989/12/31':]
ax2 = plt.subplot(1, 2, 2)
after.hist(bins=100, density=True, ax=ax2)
plt.title('after buble crushed')
plt.xlabel('$P_{t}/P_{t-1}-1$')
plt.ylabel('probability density function')
# 統計量をdfにまとめる
df = pd.DataFrame([[before.mean()[0], before.std()[0], before.skew()[0], before.kurt()[0]],
                   [after.mean()[0], after.std()[0], after.skew()[0], after.kurt()[0]]],
                   columns=['平均', '標準偏差', '歪度', '尖度'],
                   index=['バブル崩壊前', 'バブル崩壊後'])
pd.options.display.precision = 2
df

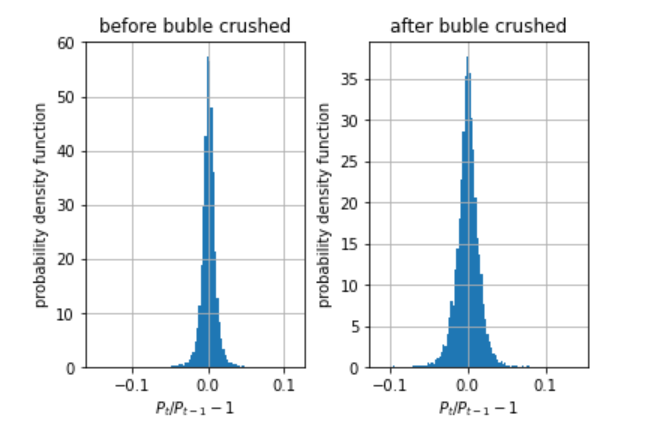
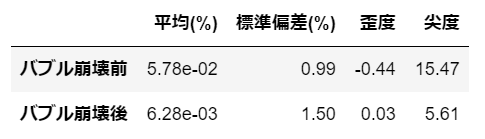
バブル崩壊前後で平均は一桁程度異なっております。標準偏差は、バブル崩壊後は崩壊前の約1.5倍に膨らんでいます。

グラフの形状をみると、バブル崩壊前は負の歪度であり、尖度が非常に高いです。一方で、バブル崩壊後は、割と正規分布に近い結果となりました。

次に、250日間隔の変化率についてバブル崩壊前後で特徴を見てみます。

# バブル崩壊前
before = chg250_N225[:'1989/12/31']
plt.figure()
ax1 = plt.subplot(1, 2, 1)
before.hist(bins=100, density=True, ax=ax1)
plt.title('before buble crushed')
plt.xlabel('$P_{t}/P_{t-250}-1$')
plt.ylabel('probability density function')
# バブル崩壊後
after = chg250_N225['1989/12/31':]
ax2 = plt.subplot(1, 2, 2)
after.hist(bins=100, density=True, ax=ax2)
plt.title('after buble crushed')
plt.xlabel('$P_{t}/P_{t-250}-1$')
plt.ylabel('probability density function')
# 統計量をdfにまとめる
df = pd.DataFrame([[before.mean()[0]*100, before.std()[0]*100, before.skew()[0], before.kurt()[0]],
                   [after.mean()[0]*100, after.std()[0]*100, after.skew()[0], after.kurt()[0]]],
                   columns=['平均(%)', '標準偏差(%)', '歪度', '尖度'],
                   index=['バブル崩壊前', 'バブル崩壊後'])
pd.options.display.precision = 2
df

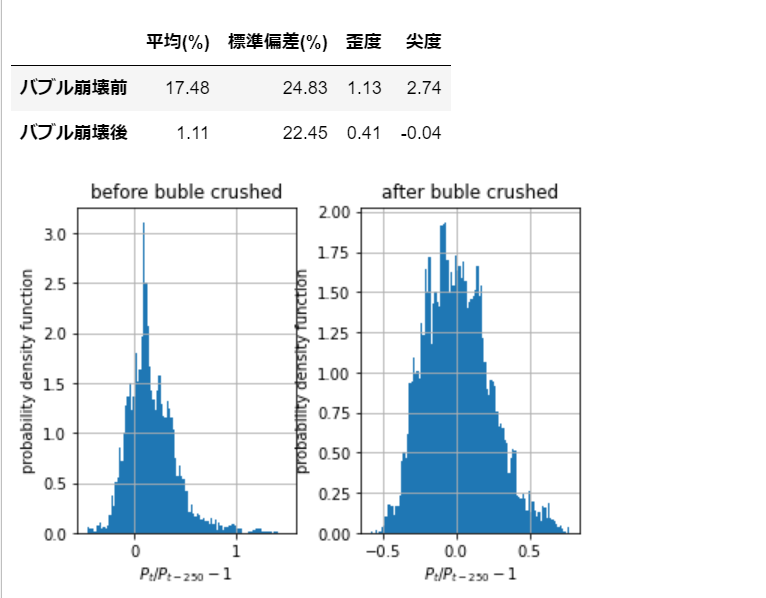
どちらの期間も正の歪度を持っていますが、バブル崩壊前の方が歪度が大きいです。これは正のフィードバックが反映されている可能性があります。バブル崩壊後は、歪度はゼロに近くなっております。

尖度は、バブル崩壊前がプラスであるのに対し、バブル崩壊後は若干マイナスとなりました。バブル崩壊前は、正規分布に近いことがわかりました。

グラフを見てみると、バブル崩壊前は、中心部分が大きく伸びているのに対し、バブル崩壊後は、ピークが複数あるように見えます。また、すそ野の広がりはバブル崩壊後の方が狭いです。

２つのヒストグラムを重ねてみます。

plt.figure()
ax3 = plt.subplot(1, 1, 1)
before.hist(bins=100, density=True, ax=ax3, label='before', histtype='step')
after.hist(bins=100, density=True, ax=ax3, label='after', histtype='step', linestyle='--')
plt.xlabel('$P_{t}/P_{t-250}-1$')
plt.ylabel('probability density function')
plt.legend()

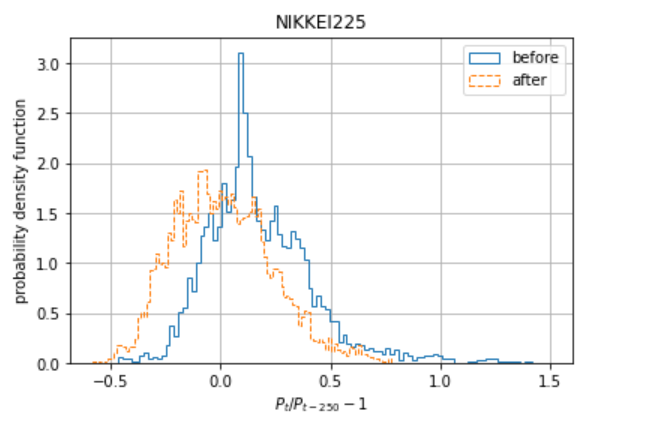
バブル崩壊後、250日変化率が大幅に下がっていることがわかります。
また、すそ野はバブル崩壊前の方がプラス方向に大きく伸びています。
このことから、バブル崩壊前の方が歪度が正に大きくなっていることがわかります。

ここまで、1日間隔と250日間隔の変化率についてみてきました。
１日間隔の変化率のヒストグラムでは、ボラティリティの違いが目に留まりました。
250日間隔の変化率のヒストグラムでは、歪度に見られるような特殊性を見ることができました。
以上から、統計的な分析だけでは不十分であり、複数期間について分析するなど経済の状態を事細かく調べる必要があります。