ARモデルによる日経平均株価の定常性分析

本記事では、ARモデルを用いる場合の基本的な流れについてまとめます。
分析対象には日経平均株価を利用しました。

今回も「Python3ではじめるシステムトレード ──環境構築と売買戦略」を参考にしております。

ARモデル
自己相関と偏自己相関
statsmodelsの利用
1. 例：日経平均株価
  1. 日経平均株価のAR(1)モデル
まとめ

ARモデル

以下の式を１次の自己回帰モデル(AR(1))と言います。

$$Z_t = \alpha + \beta Z_{t-1} + z_t$$

ここで、$z_{t}$は攪乱項です。

$| \beta | < 1$の場合、定常確率過程となります。
$\beta=1$のときは、ランダムウォークモデルです。

このモデルをさらに一般化したモデルは、ARMAモデル（自己回帰移動平均モデル）と呼ばれ、以下の式で定義されます。

$$Z_t = z_t + \sum^{p}_{i=1}\beta_i Z_{t-i} + \sum^{q}_{j=1}\gamma_j z_{t-j}$$

ここで、$i$は自己回帰の次数と呼び、$\beta_i$、$\gamma_j$はそれぞれ自己回帰係数、移動平均係数です。
$z_t$は平均ゼロ、分散$\sigma_z^2$かつ異なる次数間における共分散ゼロの攪乱項です。
これをホワイトノイズとも呼びます。
また、$q=0$の時は自己回帰モデルAR(p)、$p=0$のときは移動平均モデルMA(q)となります。

自己相関と偏自己相関

AR(p)モデル、MA(q)モデルまたはARMA(p, q)モデルのどのタイプを使ったらよいのか。
また、p, qの次数はどのように決めたらよいのか。

上記の問いは、ARMAモデルの次数の決定は自己相関と偏自己相関のグラフを用いて判断することができます。

一般に自己相関関数(autocorrelation function: acf)は次の式で与えられます。

$$acf = \frac{cov(Z_t, Z_{t-k})}{\sqrt{var(Z_t) var(Z_{t-k})} }$$

また、偏自己相関は以下のように定義されます。

$r_{12,3}$を$Z_{t-2}$を固定した場合の$Z_t$と$Z_{t-1}$の相関
$r_{13,2}$を$Z_{t-1}$を固定した場合の$Z_t$と$Z_{t-2}$の相関
$r_{23,1}$を$Z_t$を固定した場合の$Z_{t-1}$と$Z_{t-2}$の相関

グラフで判断する際は、次の表が目安となります。

モデル	自己相関	偏自己相関
AR(p)	指数関数的な減衰、または上下動の動き	大きな突出的な動きが p次まで続く
MA(q)	大きな突出的な動きが q次まで続く	指数関数的な減衰
ARMA(p, q)	指数関数的な減衰	指数関数的な減衰

statsmodelsの利用

statsmodelsのplot_acfとplot_pacfを用いることで、標本自己相関と標本偏自己相関やその信頼区間をプロットすることができます。

標本自己相関と標本偏自己相関の棒グラフの外側に信頼区間がプロットされると帰無仮説を棄却することが難しい（回帰係数がゼロである可能性が高い）です。

一方、信頼区間から標本自己相関と標本偏自己相関の棒グラフが大きくはみ出していれば、標本自己相関と標本偏自己相関はゼロでない可能性が高いと判断されます。

例：日経平均株価

1949年以降から直近までの日経平均株価の対数を用いて、次数5000までの標本自己相関と、次数40までの標本偏自己相関をプロットしてみます。

import pandas as pd
import pandas_datareader.data as pdr
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import statsmodels.api as sm
# 日経平均株価のデータを取得
N225 = pdr.DataReader('NIKKEI225', 'fred', '1949/5/16').dropna()
ln_N225 = np.log(N225)
# グラフを書く
fig = plt.figure(figsize=(8, 2))
ax1 = fig.add_subplot(1, 2, 1)
fig = sm.graphics.tsa.plot_acf(ln_N225.squeeze(), lags=5000, color='lightgray', ax=ax1)
ax2 = fig.add_subplot(1, 2, 2)
fig = sm.graphics.tsa.plot_pacf(ln_N225.squeeze(), lags=40, color='lightgray', ax=ax2)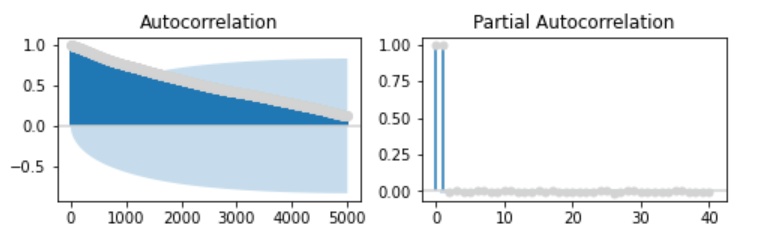

まず、標本自己相関のグラフ(左側)を見てみる。次数1500程度までは、上向きの棒グラフ(濃い青色)は信頼区間(薄い青色)の外側の棄却域にあります。
したがって有意な正の自己相関が存在する可能性が高い。

次に、標本偏自己相関のグラフ(右側)を見てみます。
グラフからはなだらかな指数関数的な減衰は減衰は見られず、２つの大きな突起（青色の棒）が見られます。2本目の突起は、１次の偏自己相関です。
したがって、上で紹介した表に基づくと、AR（１）である可能性が高いです。

日経平均株価のAR(1)モデル

　前回の記事では、日経平均株価のADF検定では、ドリフト付きモデルではランダムウォークモデルであるとみなすことが難しいという結果が得られました。

そこでドリフト付きAR（１）であるか調べてみます。

#AR(1)モデル
arma_mod = sm.tsa.ARMA(ln_N225, order=(1, 0))   # AR(1)に設定
arma_results = arma_mod.fit(trend='c', disp=-1) # c：切片付き
print(arma_results.summary())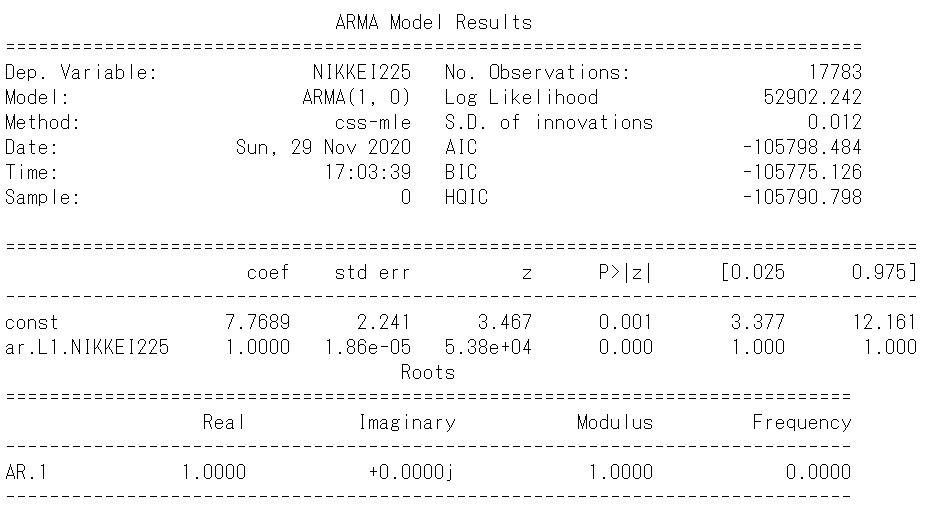

切片が7.7689で回帰係数は1であり、それぞれのp値はゼロであるので、ドリフト付きAR(1)モデルでランダムウォークである可能性が高いです。

この結果は、前回の結果と矛盾しています。
そこで線形回帰に必要な次の条件について、１つずつ確認していきます。

回帰関数は線形でなければならない
$Z_i$は確率変数であってはならない
$z_i$の平均はゼロ
$z_i$の分散は一定
$z_i$と$z_{i+j}$の相関はゼロ
$z_i$と$Z_i$の共分散はゼロ

線形性について(1)

　AR(1)は線形モデルであるため、問題なし。

残差の平均について(2)

残差の平均が一定であるかどうかグラフを用いて判断をしてみます。
その判断基準として信頼区間を用意します。
母分散が明確ではなく、標本数も十分でない場合は、スチューデントのt分布から信頼区間を求めることができます。

50日移動平均の最大値と最小値が信頼区間内に入っているか判断してみる。

#　残差の平均の信頼区間
from scipy.stats import t
resid = arma_results.resid[1:]
m = resid.mean()
v = resid.std()
resid_max = pd.Series.rolling(arma_results.resid, window=250).mean().max() # 250日移動平均の最大値
resid_min = pd.Series.rolling(arma_results.resid, window=250).mean().min() # 250日移動平均の最小値
print('平均:                 {0:.4f}, 標準偏差:             {1:.4f}'.format(m, v))
print('250日移動平均の最大値:{0:.4f}, 250日移動平均の最小値:{1:.4f}'.format(resid_max, resid_min))
print('250日平均の95％信頼区間: ', (t.interval(alpha=0.95, df=250, loc=0, scale=v))) #df:標本数, loc：平均, scale：標準偏差

250日平均の信頼区間は、[-0.02432, 0.2432]であり、最大値、最小値ともに95％信頼区間内にあります。
したがって全期間において残差の250日平均はゼロである可能性が高いです。

つまり一定であることが確認されました。

残差分散・標準偏差は一定(3)

残差をプロットしてみた結果は以下の通りです。

# 残差をプロットする
arma_results.resid.iloc[1:].plot(figsize=(6, 4), color='seagreen')
plt.ylabel('$\hat{z_t}$')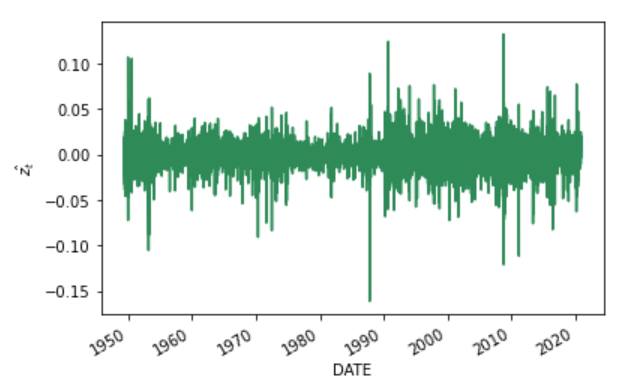

上図からバブル崩壊以降に残差は大きくなっており、分散が一定という仮説(4)に反しているように思われます。

標準偏差について、平均の時と同様に信頼区間内にあるか検証してみます。

変数$u_1,…,u_i$が独立、平均が$\mu$、分散が$\sigma^2$の正規分布に従うとき、

$$\hat{\sigma^2} (n-1) \approx \sigma^2 \chi^2_{n-1}$$

が成り立つことが知られています。
ここで、$\sigma^2 = (\sum^{n}_{i=1}u_i-\overline{u})/(n-1) $です。

したがって、標本分散の信頼区間は以下となります。

$$\frac{\hat{\sigma^2}}{\chi^2_{a/2,n-1}}(n-1) < \sigma^2 < \frac{\hat{\sigma^2}}{\chi^2_{1-a/2,n-1}}(n-1)$$

# 標準偏差について
from scipy.stats import chi2
resid = arma_results.resid[1:]
m = resid.mean()
v = resid.std()
resid_max = pd.Series.rolling(arma_results.resid, window=250).std().max()
resid_min = pd.Series.rolling(arma_results.resid, window=250).mean().min()
print('平均:                 {0:.4f}, 標準偏差:             {1:.4f}'.format(m, v))
print('250日標準偏差の最大値:{0:.4f}, 250日標準偏差の最小値:{1:.4f}'.format(resid_max, resid_min))
cint1, cint2 = chi2.interval(alpha=0.95, df=249)
print('250日標準偏差の95％信頼区間: {:.4f}'.format(np.sqrt(cint1/249)*v), end='')
print('<= σ <=', end='')
print('{:.4f}'.format(np.sqrt(cint2/249)*v))

250日移動標本標準偏差は、0.1653であり、最小値は、-0.0128であることから、信頼区間から大きく外れている期間が多いです。

ちなみにグラフで確認してみると以下の通り。

pd.Series.rolling(arma_results.resid[1:], window=250).std().plot()
plt.ylabel('$std$')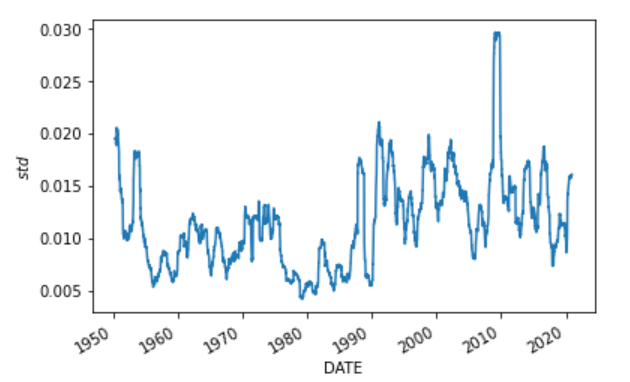

一般的に回帰分析においては分散が一定でない状態を分散不均一性といい、回帰係数の推定において問題を生じさせることが知られています。

しかし、金融市場の分散の変動は、分散不均一性以上の意味を持ちます。
金融市場では価格の変動が大きく、ジャンプしてその状態が一定期間継続することが知られています（ボラティリティのクラスタリング）。
金融市場の背後にある経済の状態そのものが変化した結果としてそのような分散の大きな変動が生じている可能性があります。
したがってこのような時には、分散不均一性というより、構造変化として認識されています。

以上を踏まえると、250日標準偏差は、分散不均一性と構造変化の可能性があるように思われます。

自己相関と偏自己相関

標本自己相関係数がゼロという帰無仮説の検定を行います。

acfでは、これについてのp値を得ることができます。
また、標本偏自己相関では95％の信頼区間を得ることができるので、これを用いて同様に帰無仮説の検定を行います。

# 自己相関・偏自己相関
from statsmodels.tsa import stattools
acf, _, p_value = stattools.acf(arma_results.resid, nlags=5, qstat=True)
pacf, confint = stattools.pacf(arma_results.resid, nlags=5, alpha=0.05) # 95%信頼区間を取得
#print('自己相関係数:', acf)
print('自己相関係数 p値:', p_value)
print('偏自己相関係数:', pacf)
print('95％信頼区間', confint)
# 偏自己相関係数が信頼区間内か判定
print( [True if value >= interval[0] and value <= interval[1] else False for value, interval in zip(pacf, confint)])

標本自己相関について、p値はすべて10％より大きいので帰無仮説を棄却することは難しいです。
したがって、標本自己相関係数は、ゼロである可能性が高いです。

同様に、標本偏自己相関についても、すべて95％信頼区間内にあるので標本偏自己相関係数もゼロである可能性が高いです。

ADF検定

残差項が定常過程が調べてみます。

# ADF検定
p1 = sm.tsa.adfuller(arma_results.resid, regression='nc')[1] # ドリフト無し
p2 = sm.tsa.adfuller(arma_results.resid, regression='c')[1] # ドリフト付き
print('ドリフト無しランダムウォーク p値:{}'.format(p1))
print('ドリフト付きランダムウォーク p値:{}'.format(p2))