本記事では、前回に引き続き「トレンドのモデル化」について「Python3ではじめるシステムトレード ──環境構築と売買戦略」で勉強したことやそれに関連することを整理します。
前回の記事では、1949年から現在までの期間で日経平均株価のトレンドのモデル化を試みました。
結果としては、決定係数の高い回帰係数は作ることができたものの、残差項の分布に着目してみると、短い期間でトレンドが発生している様子が見えました。
今回は、期間を複数に分けて、期間ごとの日経平均株価のトレンドをモデル化してみます。
期間の分け方は、以前も紹介した、内閣府が公表している景気の分類をベースに下表のように分けたものを使用します。
| 循環期 | 景気 | 期間-始点 | 終点 |
| 1, 2 | 戦後復興期(recover) | 1949/5/16 | 1954/11/30 |
| 3, 4, 5, 6 | 高度経済成長気(growth) | 1954/12/1 | 1971/12/31 |
| 7, 8, 8, 10 | 安定期(stable) | 1972/1/1 | 1986/11/30 |
| 11 | バブル経済期(bubble) | 1986/12/1 | 1993/10/31 |
| 12, 13, 14, 15,16 | 経済変革期(reform) | 1993/11/1 | 2019/11/30 |
| 独自設定 | 新型コロナウィルス期(covid-19) | 2019/12/1 | 現在(2020/11/25) |
戦後復興期
import pandas_datareader.data as pdr
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# データ取得
N225 = pdr.DataReader('NIKKEI225', 'fred', '1949/5/16').dropna()
ln_N225 = np.log(N225)
# 戦後復興期(~1954年)
y = ln_N225[:'1954/11/30'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
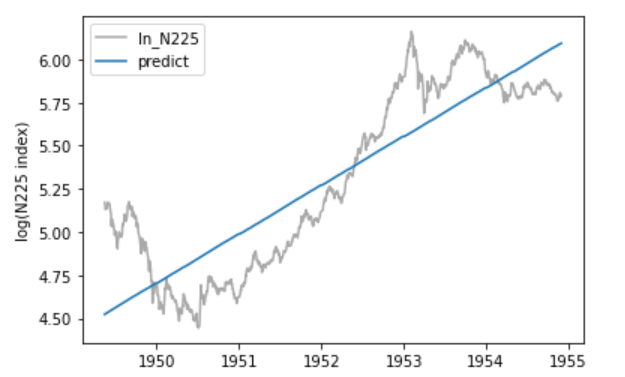
決定係数は0.762と全期間の時の値(0.756)より改善しました。
また、p値から「回帰係数と切片についてゼロである」という帰無仮説が棄却されるため、この2つの推定値については意味があります。
グラフを見てみると、山と谷が一致していない為、さらに期間を分割する必要があるように思えます。
高度経済成長期
# 高度経済成長期(1954年~1971年)
y = ln_N225['1954/12/1':'1971/12/31'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()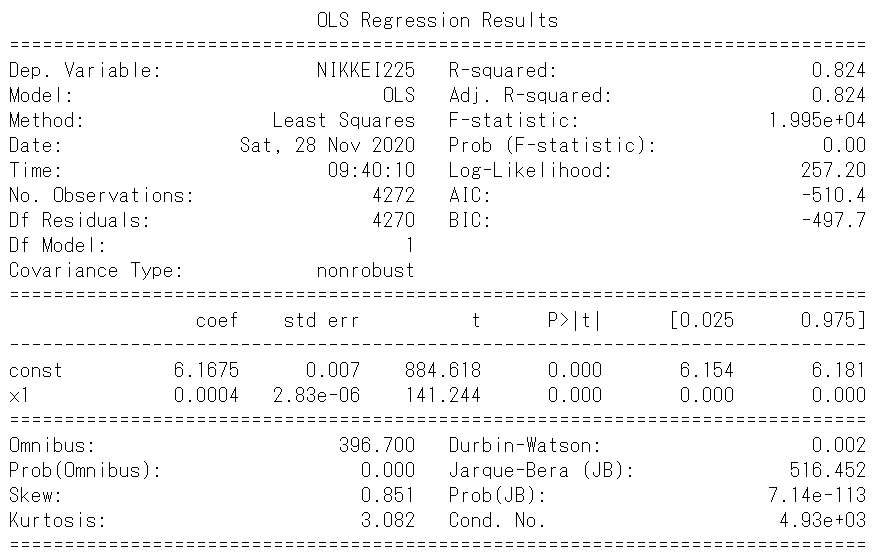
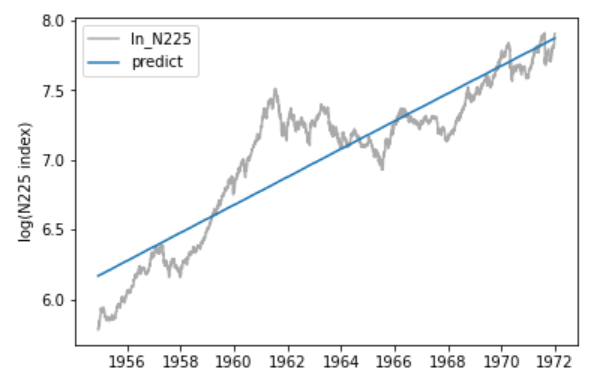
証券不況の間、日経平均株価は低迷していたことがわかります。
上図をさらに、証券不況まで、証券不況下、その後の回復期間に分けることで時間トレンドを日経平均株価の動きで説明できそうに見えます。
安定期
# 安定期(1972年~1986年)
y = ln_N225['1972/1/1':'1986/11/30'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
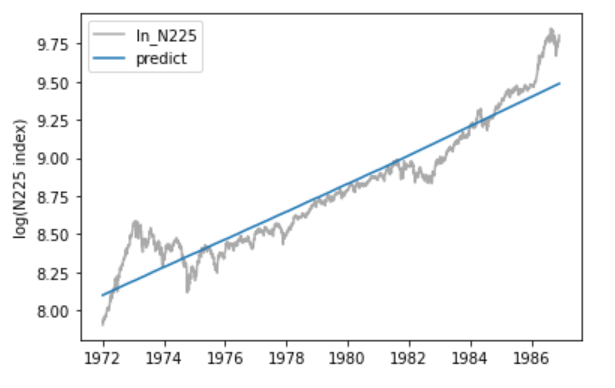
決定係数は、0.91とかなり良好です。チャートを見てみると、安定した上昇トレンドであることがわかります。
バブル成長期
# バブル成長期(1986年~1993年)
y = ln_N225['1986/12/1':'1993/10/31'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
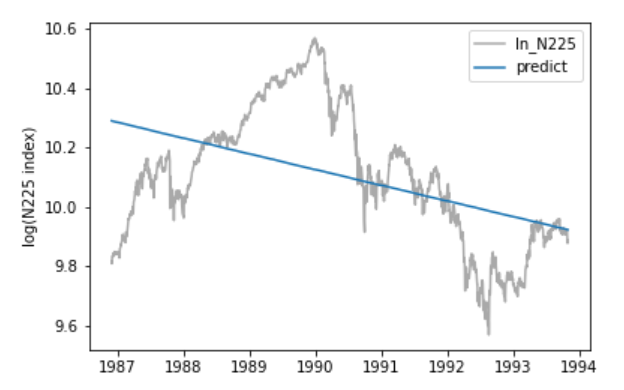
決定係数は、0.215とこれまでで一番低いです。バブルによる上昇相場とバブル終戦による暴落相場を含んでいるため、低くなっているようです。チャートを見てみると、バブルのピーク前後でトレンド形成の仕方が異なっています。したがって、これらの期間を更に分割する必要があります。そこで次では二つに分けてみました。
バブル成長期(日経平均株価ピークまで)

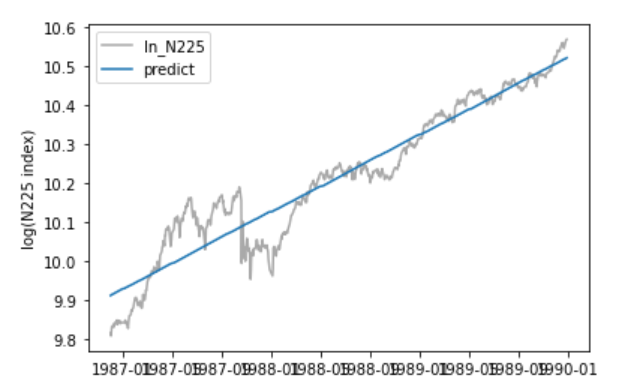
回帰係数は、これまでで一番高く強い上昇トレンドが在るように見えます。グラフからもその様子が伺えます。さらに、残差についてみてみます。
# 残差のヒストグラム
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.hist(results.resid, bins=10, color='lightgray')
plt.ylabel('frequency')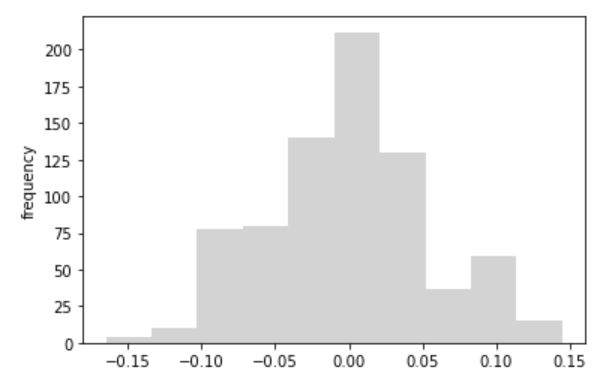
残差は一つの分布に従い、平均・分散は一定しているように見えます。
バブル暴落時(日経平均株価のピーク以降)
上記と同様の手順で、バブル暴落時の様子を見てみます。
# バブル成長期(ピークまで)
y = ln_N225['1990/1/1':'1992/8/31'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
# 残差のヒストグラム
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.hist(results.resid, bins=10, color='lightgray')
plt.ylabel('frequency')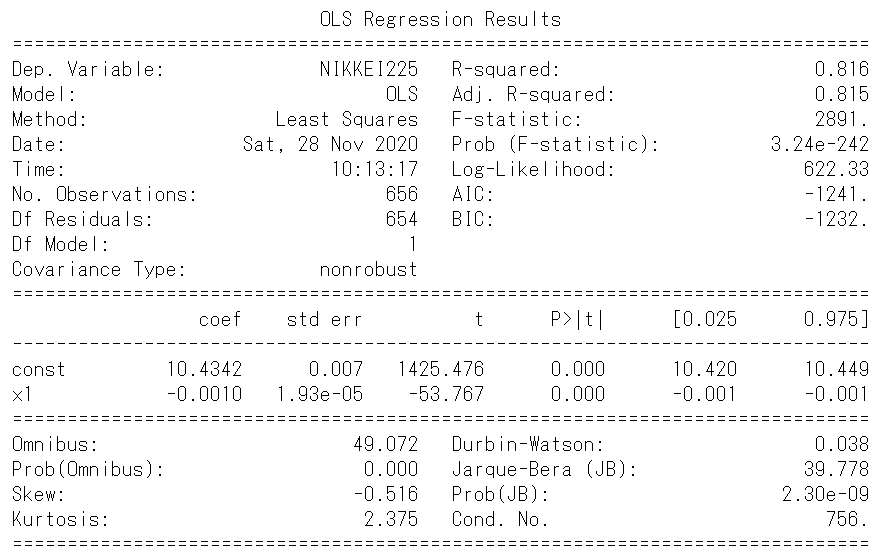
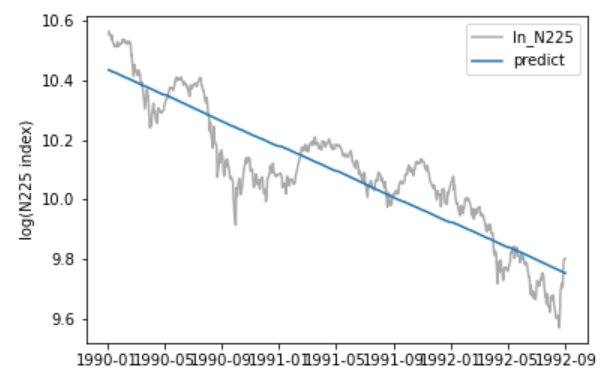
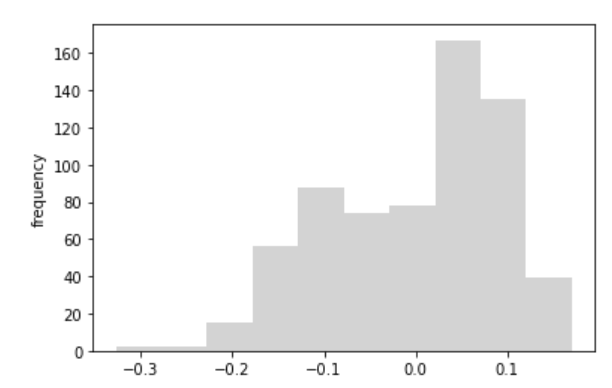
決定係数は、0.816と悪くないです。グラフを見ても、回帰モデルとしては良好に見えます。しかし、残差についてみてみると、一つの分布に従っているようには思えないです。
経済変革期
# 経済変革期(1993年~2019年11/30)
y = ln_N225['1993/11/1':'2019/11/30'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
# 残差のヒストグラム
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.hist(results.resid, bins=10, color='lightgray')
plt.ylabel('frequency')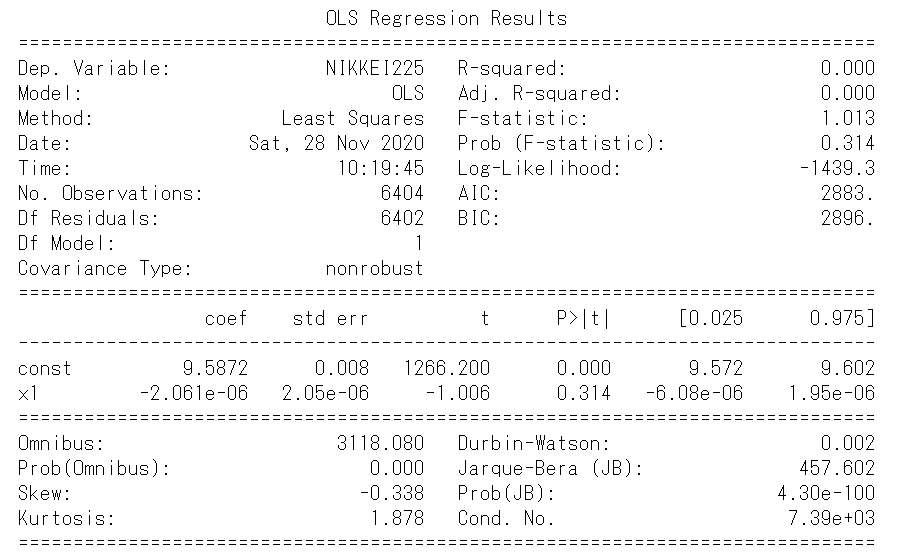
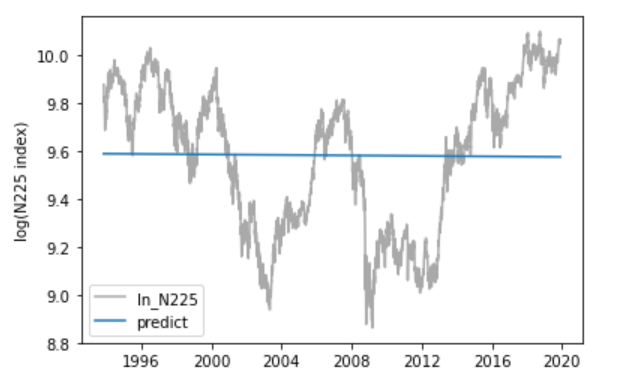
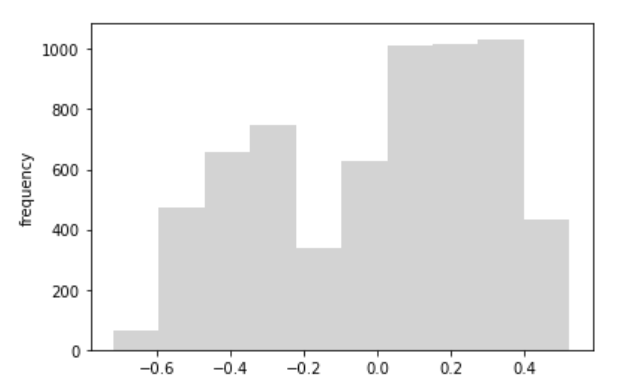
結果はこれまでで一番悪いです。決定係数は、0.0と作成したモデルは一切説明できていないことを表しています。チャートを見ても期間の取り方が適切でないことがわかります。残差のヒストグラムでもいくつかの分布から構成されていると考えられます。したがって、期間をさらに短くすることで、時間トレンドで日経平均株価を説明できる可能性があるように思えます。
新型コロナウイルス期
# 新型コロナウイルス期(2019年12/1~現在)
y = ln_N225['2019/12/1':] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
# 残差のヒストグラム
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.hist(results.resid, bins=10, color='lightgray')
plt.ylabel('frequency')
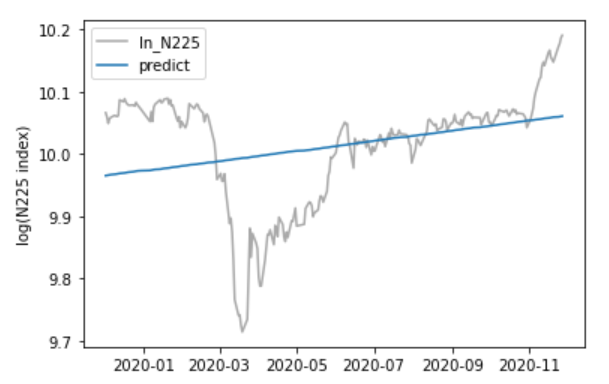
この期間についても、先ほど同様、良い結果は得られませんでした。チャートを見ると、2020年3月19日までの大暴落とそれ以降で分割する必要があるように思えます。
新型コロナウイルス期(暴落まで)
# 新型コロナウイルス期(2019年12/1~2020/3/19)
y = ln_N225['2019/12/1':'2020/3/19'] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
# 残差のヒストグラム
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.hist(results.resid, bins=10, color='lightgray')
plt.ylabel('frequency')
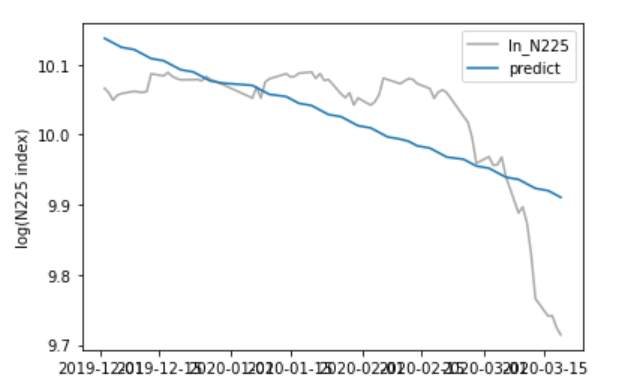
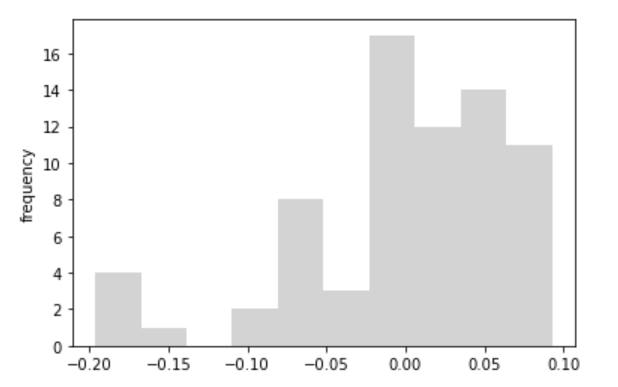
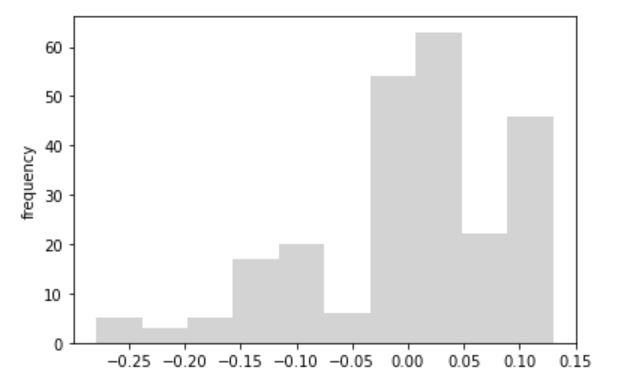
決定係数は、0.48とあまり良くないです。チャートを見ても、暴落前と暴落時でさらに分割が必要そうです。残差のヒストグラムも分布は一つではなく、平均・分散も安定して異なっています。
新型コロナウイルス期(暴落後~現在)
# 新型コロナウイルス期(2020/3/19~現在)
y = ln_N225['2020/3/19':] # 被説明変数
x = range(len(y)) # 説明変数
x = sm.add_constant(x) # 切片
model = sm.OLS(y, x) # 最小二乗法
results = model.fit()
print(results.summary())
# グラフを図示
plt.figure()
ax = plt.subplot(1, 1, 1)
plt.plot(y, label='ln_N225', color='darkgray')
plt.plot(y.index, results.fittedvalues, label='predict')
plt.ylabel('log(N225 index)')
plt.legend()
# 残差のヒストグラム
plt.figure()
ax = plt.subplot(1, 1, 1)
ax.hist(results.resid, bins=10, color='lightgray')
plt.ylabel('frequency')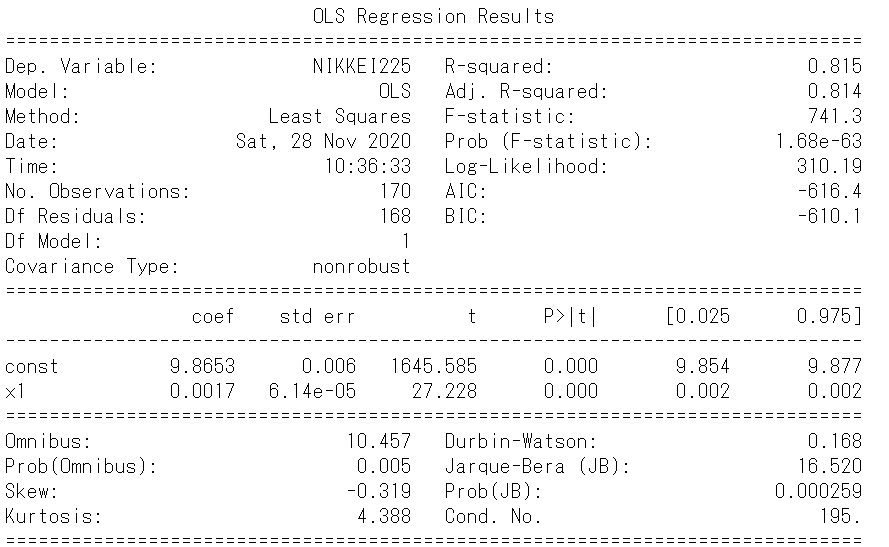
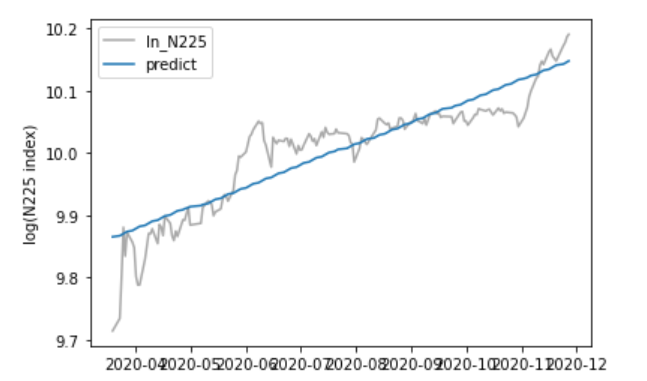
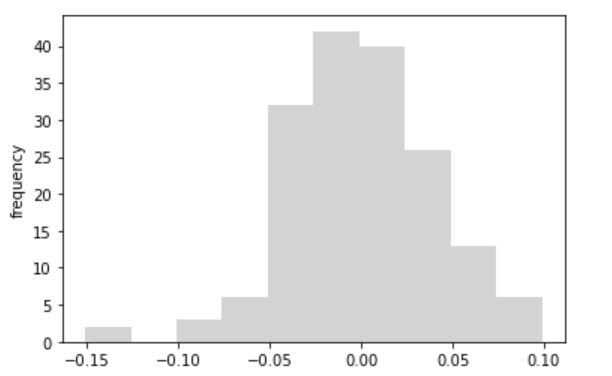
決定係数は0.815で結果は良好であるように見えます。回帰係数、切片については、ゼロである帰無仮説を棄却し、意味のある推定値であることがわかります。また、回帰係数は9.87と高く、バブルのころに匹敵するほどの上昇トレンドが見られます。残差のヒストグラムもひとつの分布から形成されており、残差の平均・分散は一定しています。したがって、安定した上昇トレンドが確認されました。
まとめ
今回は日経平均株価を景気循環における期間に分け、それぞれの期間におけるトレンドをモデル化してみました。今回の検証を通して主に以下の2点がわかりました。
- 期間幅を適切に設定することで、トレンドをモデル化することができる
- 決定係数が高くても、残差の分布についても確認する必要がある



コメント