前回の記事は、130個ある特徴量の次元を圧縮し、主成分やクラスタごとにrespとの関係を調べました。今回は、説明変数であるrespの特徴について調べてみます。
※本記事は、公開しているNotebookをまとめたものとなっております。
データの分布
まずは、respの分布をヒストグラムにしてみます。
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import os
import matplotlib.pyplot as plt
%matplotlib inline
for dirname, _, filenames in os.walk('/kaggle/input'):
for filename in filenames:
print(os.path.join(dirname, filename))
train = pd.read_csv('/kaggle/input/jane-street-market-prediction/train.csv')
# データの分布
train['resp'].hist(bins=30)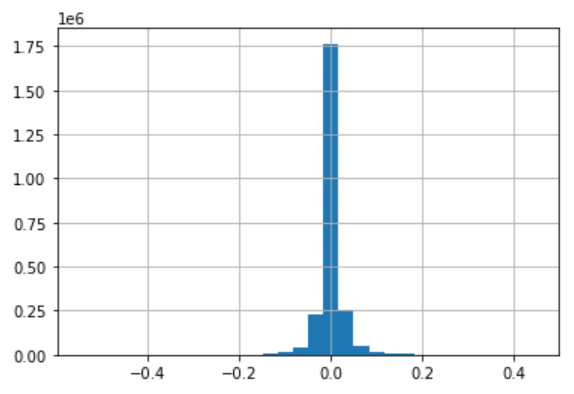
左右はほぼで対称、0近辺にデータが集中しています。
累積和の推移
次にrespの累積和の推移をプロットをしてみます。
# リターンの累積和
train['resp'].cumsum().plot(label='resp')
train['resp_1'].cumsum().plot(label='resp_1')
train['resp_2'].cumsum().plot(label='resp_2')
train['resp_3'].cumsum().plot(label='resp_3')
train['resp_4'].cumsum().plot(label='resp_4')
plt.legend()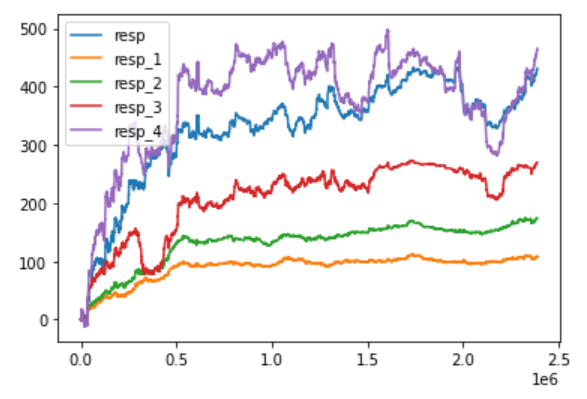
最初の50,000個のデータでは着々とリターンを積み上げており、その後はしばらく横ばいが続き、最後の50,000個でリターンが積みあがっている様子が見られます。
最初の上昇が継続している期間は、上昇トレンドが発生している可能性があります。
最初の期間の特徴をうまく抽出してあげることがパフォーマンスの良いモデルを構築するカギとなるのかもしれないです。
対数変換
説明変数を対数変換することはよくあります。
そこで、対数変換をし、データの分布をヒストグラムで描いてみます。
ただし、対数をとるだけでは、infになってしまうため、1を足しています。
np.log(train['resp']+1).hist(bins=30, color='lightblue', label='log(y)')
train['resp'].hist(bins=30, histtype='step', color='red', label='y')
plt.legend()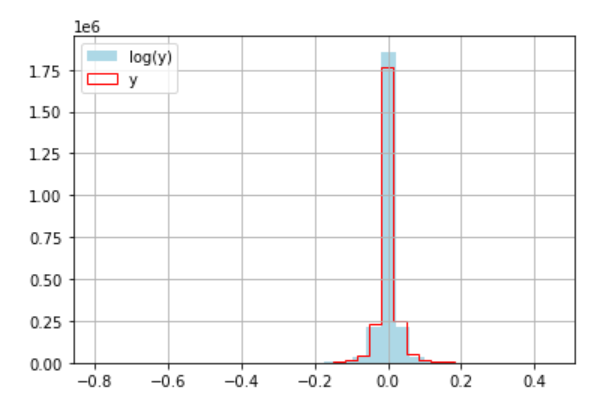
対数変換前に比べると、マイナスのばらつきが広がりました。
また、0近辺のデータが増えています。
対数変換により大して変化は見られなかったですが、目的変数に用いてみるのも良いかもしれないです。ただし、その場合は、予測値を逆変換する必要があります。
プラスとマイナスの割合
プラスとマイナスの割合を見てみます。
plt.pie(train['resp'].apply(lambda x:1 if x>0 else -1).value_counts(),
labels=['plus', 'minus'], startangle=90, autopct='%1.1f%%')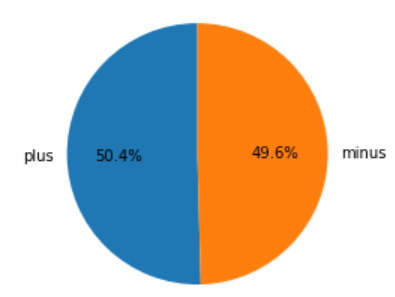
若干だがプラスのデータの方が多かったです。
学習データに用いる場合は、ほぼ1:1なので問題はなさそうです。
要約統計量
respと対数変換後のrespの要約統計量を算出してます。
train['resp'].describe()
np.log(train['resp']+1).describe()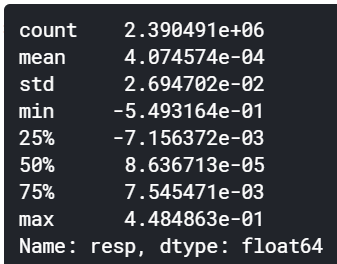
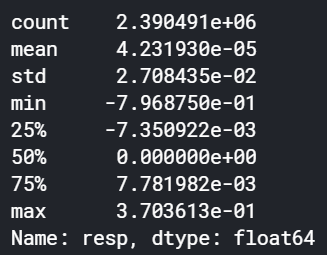
対数変換による効果はあまりなさそうです。
移動平均
ウィンドウ幅を複数指定して、移動平均の累積和をプロットしてみます。
train['resp'].cumsum().plot(label='resp')
train['resp'].rolling(window=50).mean().cumsum().plot(label='MA_50')
train['resp'].rolling(window=50000).mean().cumsum().plot(label='MA_50000')
train['resp'].rolling(window=100000).mean().cumsum().plot(label='MA_100000')
plt.legend()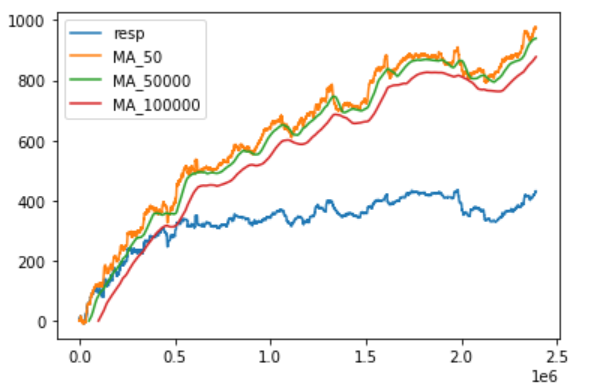
ウィンドウ幅として、50, 50000, 100000を指定してみました。
結果としては、ウィンドウ幅による差はほとんど見られなかったです。
また、移動平均の累積和は右上がりとなっていました。
50,000~150,000の期間のrespでは横ばいの傾向が見られましたが、移動平均は上昇傾向にあるようです。
次に各移動平均のヒストグラムを書いてみます。
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
train['resp'].rolling(window=50).mean().hist(bins=30)
plt.title('window=50')
plt.subplot(1, 3, 2)
train['resp'].rolling(window=50000).mean().hist(bins=30)
plt.title('window=50000')
plt.subplot(1, 3, 3)
train['resp'].rolling(window=100000).mean().hist(bins=30)
plt.title('window=100000')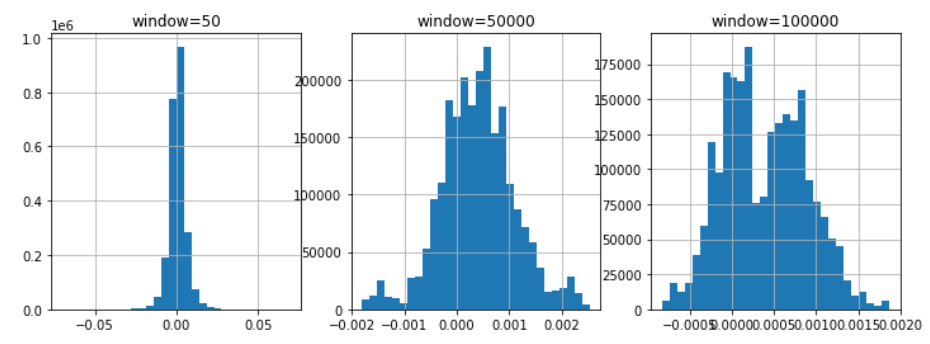
中心極限定理に基づくと正規分布に従うはずです。
window=50は正規分布に近い形をしていますが、他の分布に関しては複数の分布から構成されているように見えます。
ウィンドウの幅は関係ないようにも思えましたが、ちゃんと選ぶ必要があるのかもしれないです。
まとめ
今回はrespの特徴について簡単に調べてみました。
あまり意味のないような分析かもしれませんが、今後のモデル開発で何かしら役に立てば幸いです。


コメント