金融市場におけるモンテカルロシミュレーション

本記事では「Python3ではじめるシステムトレード ──環境構築と売買戦略」で学んだことを独自の見解を踏まてし整理します。今回のテーマは、「モンテカルロシミュレーション」です。

モンテカルロシミュレーション
まとめ

モンテカルロシミュレーション

モンテカルロシミュレーションとは、独立同一の分布に従う確率変数の和から、人工的に時系列を生成し、その性質を理解することです。

今回は、以下の3つのモデルのうち、2つ目まで検証してみます。

単純ランダムウォーク：$P_t=R_{t-1}+\sigma w_t$
AR(1)モデル：$P_t=\alpha+\beta P_{t-1}+\sigma w_t$
ベルヌーイ過程：$P_t=P_{t-1}+\sigma B_t$

ここで、$P_t$は$t$時の価格。$P_{t-1}$は$t$よりも１単位時間前の価格。
$w_t$は平均ゼロ、分散１の正規分布に従う確率変数で、$\sigma$は定数です。
$B_t$は+1, -1からなるベルヌーイ過程です。

今回のシミュレーションでは、$\sigma=0.1/\sqrt{250}=0.00632$としています。

1. ランダムウォーク

まずは、１年間の$P_t$の動きを人工的に生成してみます。
株価の初期値Pを１として、株式市場の１年間の営業日数を250日として、株価の動きを生成してみます。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
sigma = 0.1 / np.sqrt(250)
P = [1]
for i in range(1, 250):
    w = np.random.normal(0, 1)
    P.append(P[i-1] + sigma * w)

これで価格の時系列を生成することができました。

次に、価格の差分をとり、その平均、標準偏差、歪度、尖度を確かめます。
また、それに合わせて、グラフと価格変化のヒストグラムを書いてみます。

price = pd.Series(P)
diff_P = price.diff().dropna() # 価格の変化(差)
# 平均、標準偏差、歪度、尖度を表示
print('mean:{0:.4f}, std:{1:.4f}, skew:{2:.4f}, kurt:{3:.4f}'.format(diff_P.mean(),diff_P.std(), diff_P.skew(), diff_P.kurt()))
# グラフを書く
plt.figure(figsize=(8, 3))
ax1 = plt.subplot(1, 2, 1)
price.plot(color='darkgray', ax=ax1)
plt.xlabel('t')
plt.ylabel('$P_t$')
# ヒストグラムを書く
ax2 = plt.subplot(1, 2, 2)
diff_P.hist(color='lightgreen', ax=ax2)
plt.xlabel('P_t-P_{t-1}')
plt.ylabel('frequency')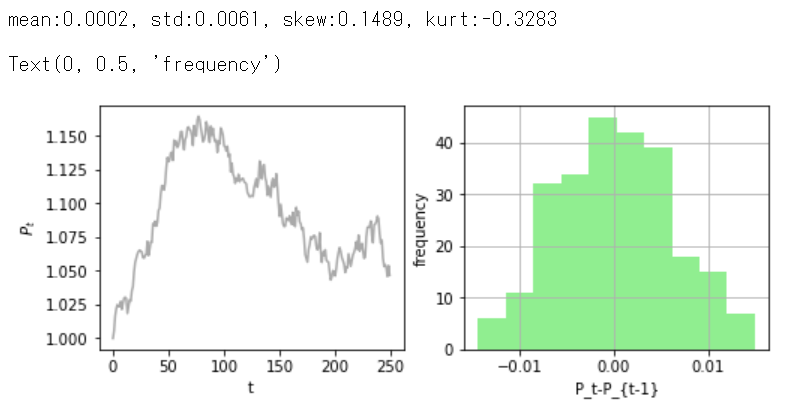

平均はゼロで標準偏差もほぼ想定通りで、歪度と尖度はほぼゼロに近いです。
ヒストグラムを見てみると、比較的綺麗な正規分布が描かれました。

次に、250個の価格データを生成した上述の過程を10,000回繰り返し、1日目～250日目の最大値、最小値を求め、その推移をグラフに書いてみます。
それにより、価格の推移の期間構造を求めてみます。
この作業は、前回の記事で日経平均株価に対して行ったものと同じです。詳細は前回の記事をご参照ください。

# 10000回シミュレーションを実施
P_250 = []
P_diff = []
high = [0]*250
low = [1]*250
for j in range(10000):
    P0 = 1
    for i in range(250):
        w = np.random.normal(0, 1)
        P0 = P0 + sigma * w
        if P0 > high[i]:
            high[i] = P0
        if P0 < low[i]:
            low[i] = P0
        P_diff.append(sigma * w)
    P_250.append(P0)
# グラフを書く
plt.figure(figsize=(9, 4))
# 推移
high = pd.Series(high)
low = pd.Series(low)
ax1 = plt.subplot(1, 2, 1)
high.plot(label='high', linestyle='--', ax=ax1)
low.plot(label='low', linestyle='--', ax=ax1)
plt.title('max$P_t$-min$P_t$')
plt.xlabel('x')
plt.ylabel('$P_t$')
plt.legend(loc='upper left')
# 250日目の価格のヒストグラム
ax2 = plt.subplot(1, 2, 2)
P_250 = pd.Series(P_250)
P_250.hist(bins=100)
plt.xlabel('$P_{250}$')
plt.ylabel('frequency')
# 平均、標準偏差、歪度、尖度を表示
print('mean:{0:.4f}, std:{1:.4f}, skew:{2:.4f}, kurt:{3:.4f}'.format(P_250.mean(),P_250.std(), P_250.skew(), P_250.kurt()))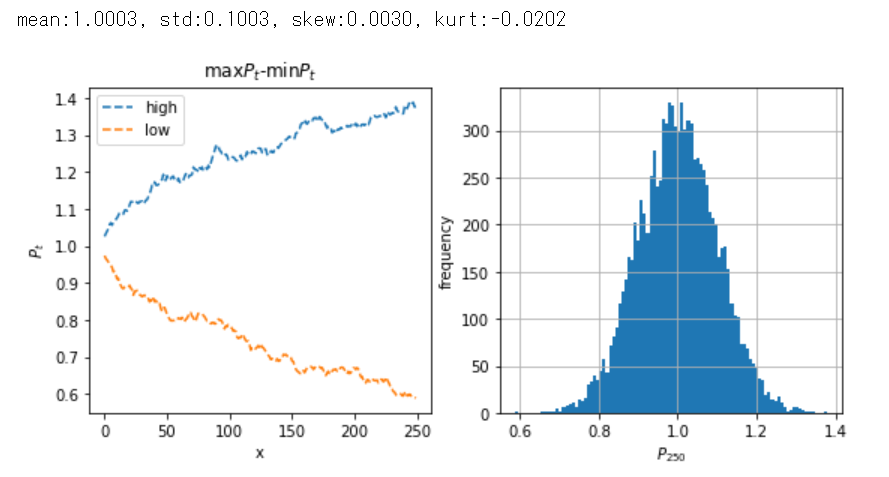

左図からは価格の最大値と最小値はほぼ直線的に伸びていることがわかります。
右図からは分布はほぼベル型であり、250日目の価格は設定どおり、平均１、標準偏差ゼロの分布にしたがっています。
歪度と尖度もほぼゼロとなっています。

前回の記事で調べた際の価格推移は以下でした。

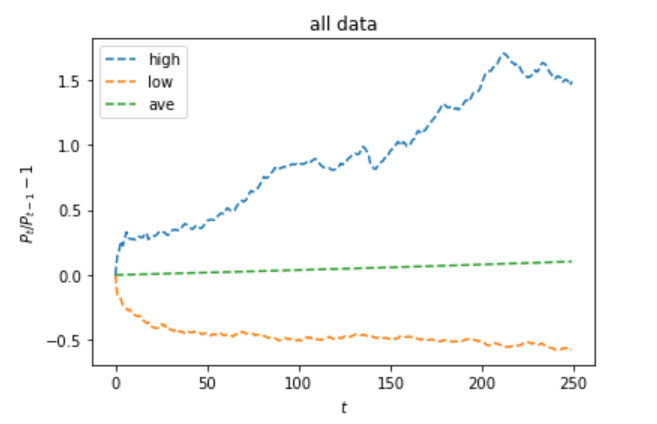
最小値(low)のグラフは割とスムーズですが、最大値(high)のグラフは凹凸した形をしています。
パラメータが一定のシミュレーションでは、現実世界を説明はできないが、似たような動きをしていることは見てとれます。

次に、得られた時系列から1日間隔の変化率とそれを１日ずらした変化率の散布図を書いてみます。

# 散布図
P_diff = pd.Series(P_diff)
plt.figure(figsize=(6, 6))
plt.scatter(P_diff, P_diff.shift(1), alpha=0.01)
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')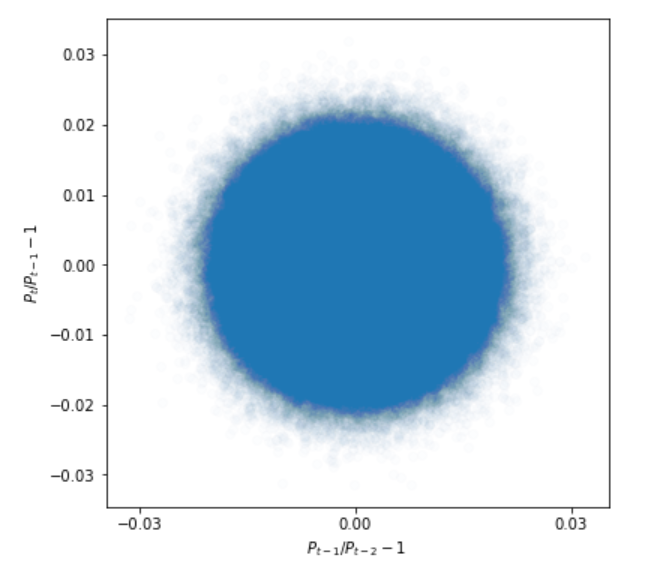

実際のデータとは異なり、丸の円が描かれました。
つまり、二つの変化率に相関が無いことがわかります。
これが分散不均一性もボラティリティクラスタリングもない世界の場合になります。

AR(1)モデル

1次の自己回帰モデルは以下の式で与えられます。

$$P_t=\alpha+\beta P_{t-1}+\sigma w_t$$

この$\beta$を指定することで、AR(1)がどのような性質を持っているか調べてみます。
$\beta$を指定することで$\alpha$を決める必要がありますが、これは期待値($\mu$から求めることができます。
AR(1)の期待値$E(P_t)$は以下で与えられます。

$$E(P_t) = E(\alpha) + E(\beta P_{t-1}) + E(\sigma w_t)$$

ここで、$E(P_t) = \mu $とすると、$E(\alpha)=\alpha $、$E(w_t)=0$であるから、

$$ \mu = \alpha + \beta \mu = \frac{\alpha}{1-\beta}$$

となります。
価格の初期値を1とすると、$\alpha = 1 – \beta $です。

分散は、

$$var(P_t) = E(P_t – \mu)^2=E(P_t^2) – \mu^2$$

であり、$\alpha=0$であれば、

$$var(P_t) = \frac{\sigma_z^2}{1-\beta^2}$$

です。

つまり期待値も分散も時間と独立しています。ここがランダムウォークとは異なる点となります。

以降の分析のために、以下のようにAR(1)の時系列を生成する関数を定義しておきます。

# AR(1)時系列生成関数を定義
def AR1(beta, sigma, n, m, p0):
    '''
    AR(1)における時系列データを生成
    beta:回帰係数, sigma:標準偏差, n:生成するデータ数, m:分析期間, p0：初期値 
    '''
    P = []
    dP = []
    high = [0] * m
    low = [p0] * m
    alpha = (1-beta)*p0
    sigma_w = sigma * p0
    for j in range(n):
        P0 = p0
        for i in range(m):
            w = np.random.normal(0, 1)
            P1 = beta * P0 + alpha + sigma_w*w
            dp = P1 - P0
            P0 = P1
            if P0 > high[i]:
                high[i] =P0
            if P0 < low[i]:
                low[i] =P0
            dP.append(dp)
        P.append(P0)
    return pd.Series(price), pd.Series(dprice), pd.Series(high), pd.Series(low)

まず初めに、beta=0.9999, sigma=0.00632, n=10000, m=250, p0=1として時系列を生成し、最大値・最小値の推移やヒストグラムを表示します。

# 時系列を生成
beta, sigma, n, m, p0 = (0.9999, 0.00632, 10000, 250, 1) # パラメータ設定
price, dprice, high, low = AR1(beta, sigma, n, m, p0)
# グラフを書く
plt.figure(figsize=(8, 4))
# 最大値と最小値の推移
ax1 = plt.subplot(1, 2, 1)
high.plot(label='high', linestyle='--', ax=ax1)
low.plot(label='low', linestyle='--', ax=ax1)
plt.title('max$P_t$-min$P_t$')
plt.xlabel('x')
plt.ylabel('$P_t$')
plt.legend(loc='upper left')
# 250日目の価格のヒストグラム
ax2 = plt.subplot(1, 2, 2)
price.hist(bins=100)
plt.xlabel('$P_{250}$')
plt.ylabel('frequency')
# 平均、標準偏差、歪度、尖度を表示
print('mean:{0:.4f}, std:{1:.4f}, skew:{2:.4f}, kurt:{3:.4f}'.format(dprice.mean(), dprice.std(), dprice.skew(), dprice.kurt()))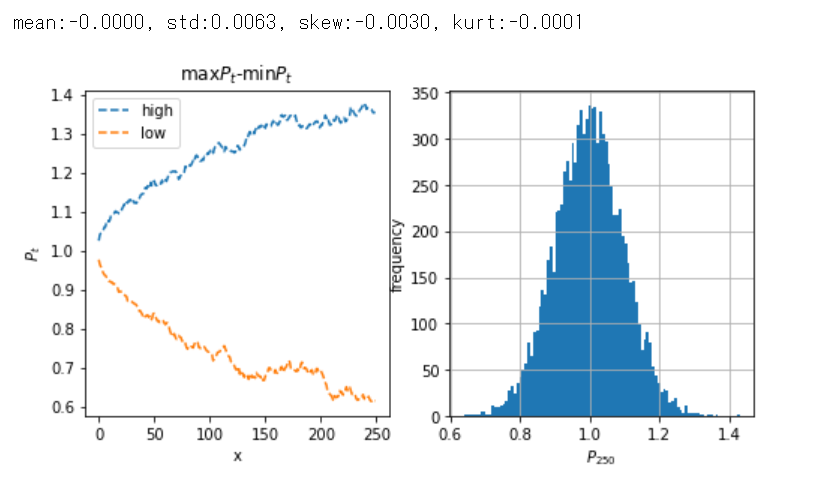

価格差の平均はゼロ、標準偏差は0.0063、歪度、尖度ともにゼロ近辺という結果になりました。
$\beta<1$である特徴がわずかに出ているかもしれませんが、ランダムウォークとほぼ同等になりました。

次に、1単位時間差について散布図を書いてみます。

# 散布図
plt.figure(figsize=(6, 6))
plt.scatter(dprice, dprice.shift(1), alpha=0.01)
plt.xlabel('$P_{t-1}/P_{t-2}-1$')
plt.ylabel('$P_{t}/P_{t-1}-1$')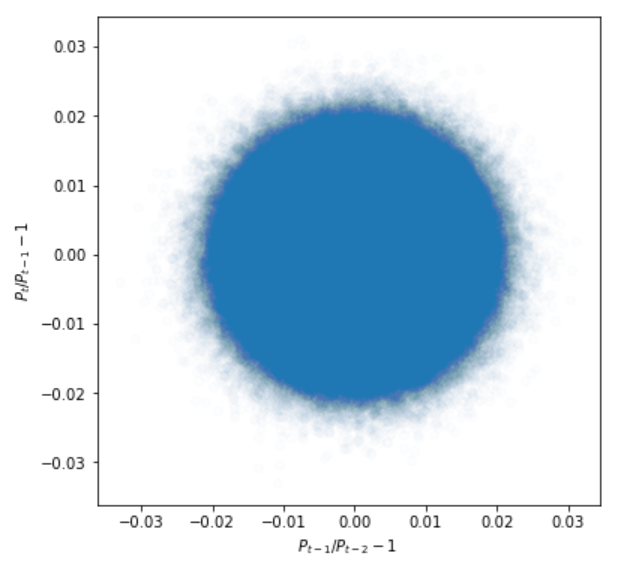

価格差は綺麗な円形を示しています。つまり、自己相関がほぼないです。

次に、AR(1)の特徴をさらに明確につかむために、$\beta$の値を動かしてみます。
今回は、$\beta=0.99, 0.5, 1.003, 1.005, 1.01$として実験をしてみます。

$\beta=0.99$の場合

# 時系列を生成
beta, sigma, n, m, p0 = (0.99, 0.00632, 10000, 250, 1) # パラメータ設定
price, dprice, high, low = AR1(beta, sigma, n, m, p0
# 以下省略 #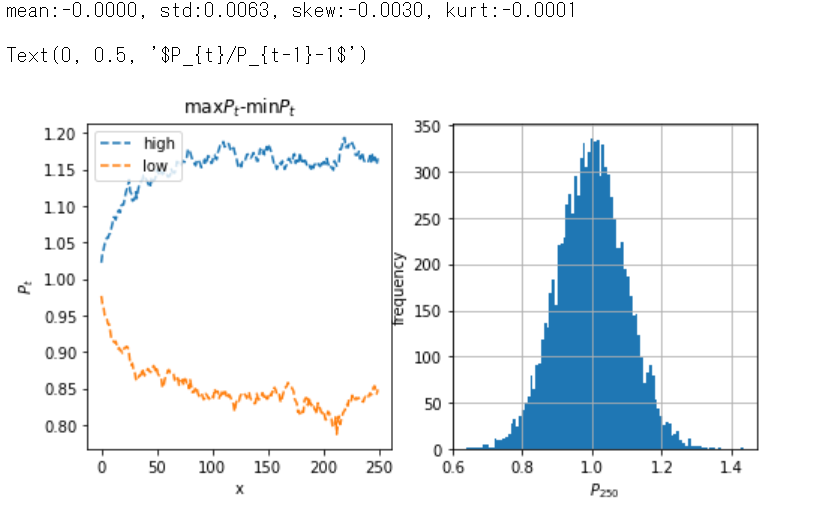

結果は、価格差の平均はゼロ、標準偏差は0.0063、歪度と尖度はほぼゼロとなりました。
$\beta=0.99$では、ある日数を経過と、価格の最大値と最小値の幅が一定値にとどまる様子が見られます。
これが、中心回帰、定常確率過程の特徴らしいです。
それでも定常性を得るために、50日程度かかっていることがわかる。

$\beta=0.5$の場合

次に、$\beta=0.5$にしてみます。

# 時系列を生成
beta, sigma, n, m, p0 = (0.5, 0.00632, 10000, 250, 1) # パラメータ設定
price, dprice, high, low = AR1(beta, sigma, n, m, p0)
# 以下省略 #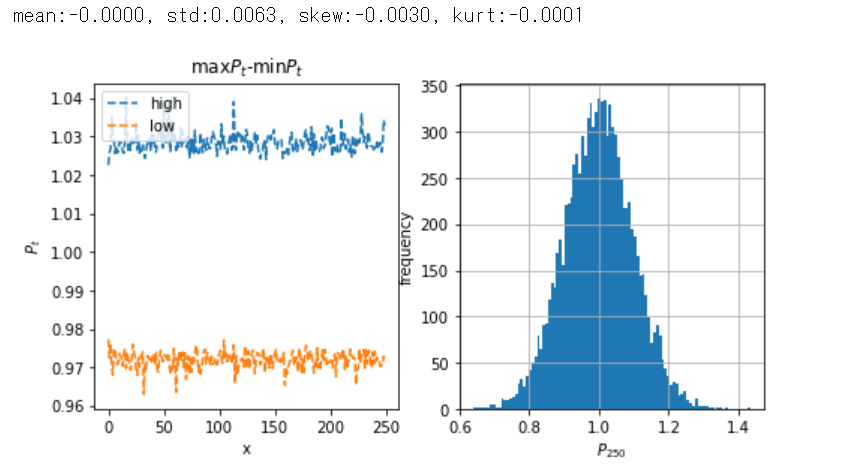

結果は、価格差の平均はゼロ、標準偏差は0.0063、歪度と尖度はほぼゼロとなりました。
$\beta=0.5$ではほぼ主運管的に中心回帰の定常確率過程の特徴が見えてきます。

$\beta=1.003$の場合

次に、AR(1)が発散する場合($\beta>1$として$\beta=1.003$を見てみます。

# 時系列を生成
beta, sigma, n, m, p0 = (1.003, 0.00632, 10000, 250, 1) # パラメータ設定
price, dprice, high, low = AR1(beta, sigma, n, m, p0)
# 以下省略 #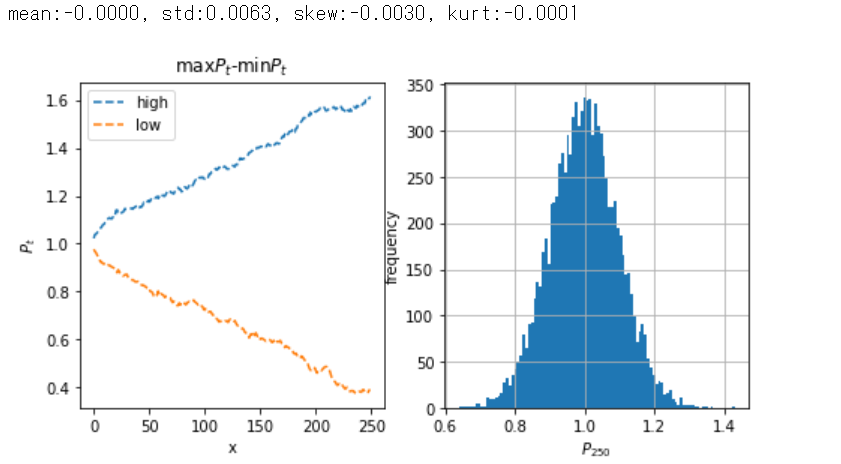

　結果は、価格差の平均はゼロ、標準偏差は0.0063、歪度と尖度はほぼゼロとなった。$\beta=1.003$ではまだ発散に至っておらず、ランダムウォークとの区別が難しいです。

$\beta=1.005$の場合

$\beta=1.005$にしてみます。

# 時系列を生成
beta, sigma, n, m, p0 = (1.005, 0.00632, 10000, 250, 1) # パラメータ設定
price, dprice, high, low = AR1(beta, sigma, n, m, p0)
# 以下省略 #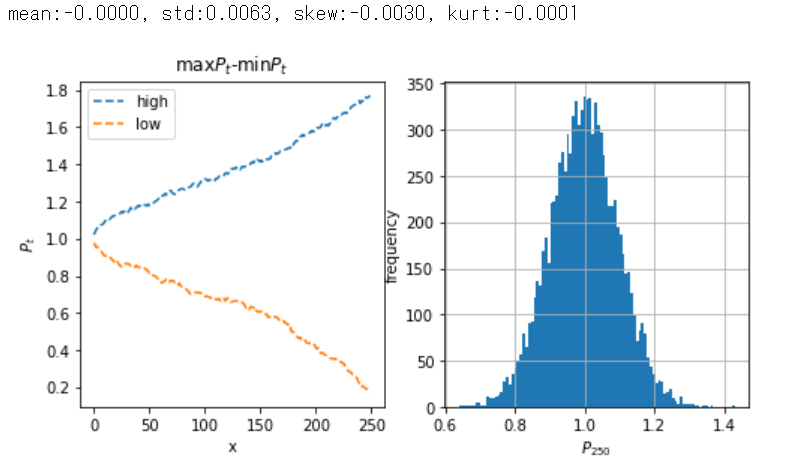

結果は、価格差の平均はゼロ、標準偏差は0.0063、歪度と尖度はほぼゼロとなりました。
$\beta=1.005$では発散の一歩手前である様子が見られます。

$\beta=1.01$の場合

最後に$\beta=1.01$にしてみます。

# 時系列を生成
beta, sigma, n, m, p0 = (1.01, 0.00632, 10000, 250, 1) # パラメータ設定
price, dprice, high, low = AR1(beta, sigma, n, m, p0)
# 以下省略 #S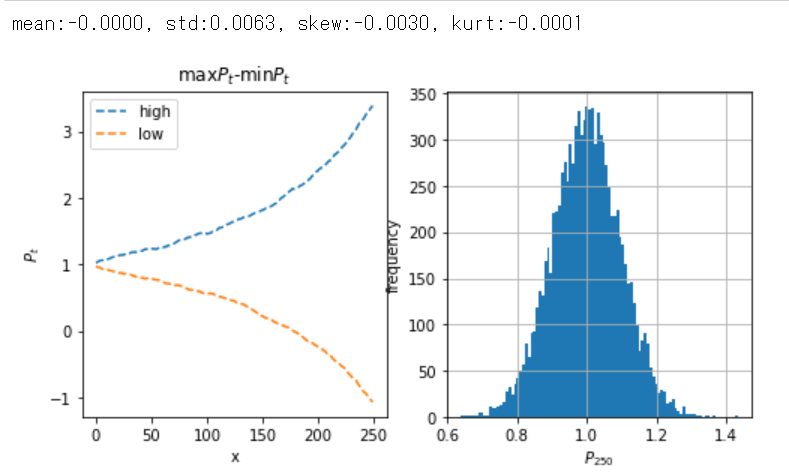

結果は、価格差の平均はゼロ、標準偏差は0.0063、歪度と尖度はほぼゼロとなりました。
$\beta=1.01$では発散する様子を見ることができました。

AR(1)まとめ

AR(1)モデルについてここまで(\beta\)を何通りか動かしシミュレートしてみました。
$\beta>1$であってもその程度が小さければ、価格過程は破綻することが無いことがわかりました。
また、それは観測期間にも左右される様子が見られました。
期間が短ければ、$\beta$が1よりも大きくても破綻せずに済む確率は上がります。
また、$\beta<1$近辺では、ランダムウォークとの区別が難しい結果となりました。

自己回帰モデルの最大の特徴は、価格の中心回帰の動きです。
ランダムウォークの価格の動きは時間の経過と共に分散が大きくなるのに対して、自己回帰モデルではある点に収束します。その為、将来予測を行うためには便利です。
(↑ 価格の変化幅が一定に収まるため?)

ベルヌーイ過程

最後にベルヌーイ過程についてシミュレートしてみます。
結果が二つしかない実験をベルヌーイ試行と呼び、とびとびの値からなる独立な離散時間の確率変数列をベルヌーイ過程と呼びます。

今回は、とりうる二つの値を{-5, +5}として1万個の確率変数を発生させ、その和を一日分の取引とします。
まずは、以下の通り、生成器を関数で定義し、試しに価格の推移をグラフにしてみます。

#ベルヌーイ過程に基づく価格を生成
def bernoulli(N, p0):
    #N：個数、p0：価格の初期値
    s = (np.random.binomial(1, 0.5, N)-0.5) * 10 # -0.5 or 0.5の乱数をn個生成後、10を書けることで{-5, +5}にしている
    P = [p0]
    for i in range(N):
        P.append(P[i] + s[i])
    return pd.Series(P)
P = bernoulli(10000, 0)
# 価格推移を書く
plt.figure(figsize=(8, 4))
P.plot(color='darkgray')
plt.xlabel('step $t$')
plt.ylabel('$\sum_{1}^{t} B_t \cdot 5$')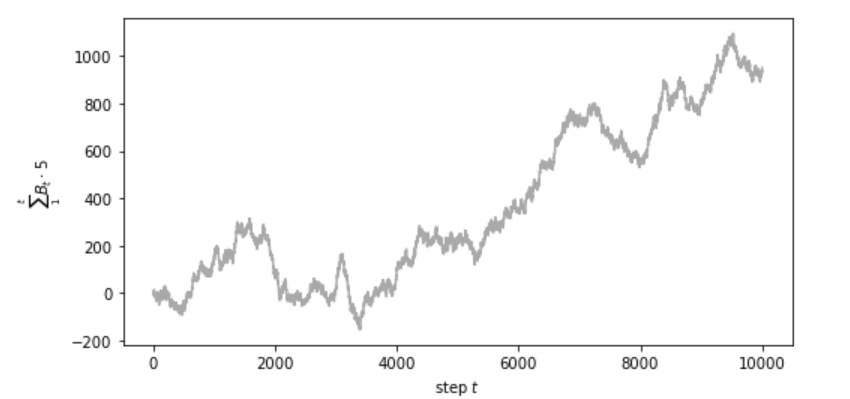

実際の価格の動きに似たものを再現できています。
これはランダムウォークであり、一定方向に価格が上昇したり下落しているのは確率的トレンドです。

次にこの実験を10000回繰り返し、それぞれの試行で生成した確率変数の和をヒストグラムにしてみます。

N = 10000
M = 10000
Q = []
for j in range(M):
    P =bernoulli(N, 0)
    Q.append(P[N])
plt.figure()
plt.hist(Q, density=True, bins=25)
plt.xlabel('$\sum_{1}^{t} B_t \cdot 5$')
plt.ylabel('probility deinsity function')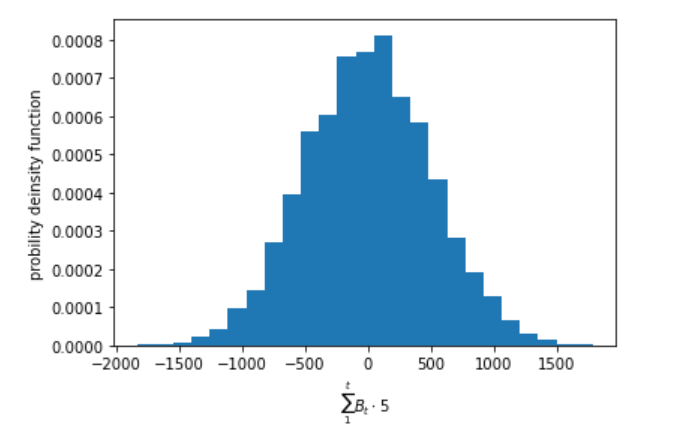

結果は、正規分布に近いベル型の形となりました。

次に1日の取引回数を3000回に減らしてみます。

N = 3000
M = 10000
Q = []
for j in range(M):
    P =bernoulli(N, 0)
    Q.append(P[N])
plt.figure()
plt.hist(Q, density=True, bins=25)
plt.xlabel('$\sum_{1}^{t} B_t \cdot 5$')
plt.ylabel('probility deinsity function')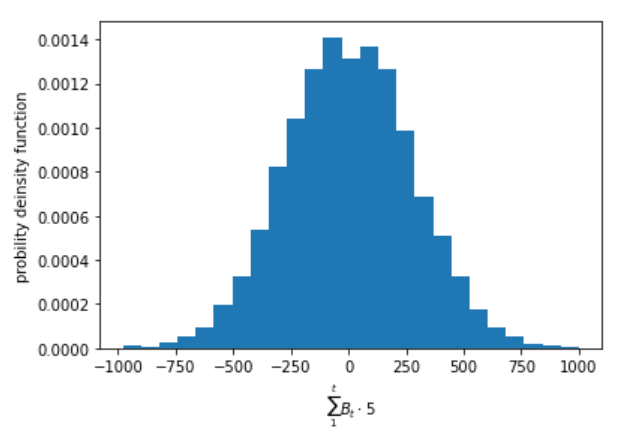

結果として、分布の幅が狭くなっていることがわかります。
つまり、一日の価格の動きが取引回数に依存していることがわかります。
また、先ほどに比べ分布の滑らかさが維持されていないことにも気が付きます。
つまり、ボラティリティは取引数と関係があることがシミュレーションを通してもわかりました。

まとめ

今回は、単純ランダムウォーク、ARモデル、ベルヌーイ過程の３つのモデルについてモンテカルロシミュレーションを試してみました。

単純ランダムウォークのシミュレーションでは、実際の日経平均株価と比較し、現実の価格推移と似たような動きをすることが確認できました。

ARモデルでは、$\beta$の値をいろいろ動かしてみてその特性についてみてみました。
回帰係数からそのモデルの特徴を掴むのは難しいですが、シミュレーションを通して視覚的にARモデルについて理解を深めることができたのではないかと思います。
この点がモンテカルロシミュレーションを行ってみるメリットの一つと感じました。

ベルヌーイ過程では、シミュレーションを通してボラティリティと取引数の関係性についてみることができました。

仮定が成立しない現実世界ではシミュレーション通りになることは滅多にないです。
しかし、仮説が成立した場合にモデルがどのような特性を持つか知っておくことは非常に大切なことです。モデルの特性を理解しておくことで分析結果に対してより深い考察ができるようになると思います。

以上、モンテカルロシミュレーションを利用した検証の紹介でした。