本記事では、「Python3ではじめるシステムトレード ──環境構築と売買戦略」で紹介されていた便利な関数を備忘録として残しておきます。本書とは、一部コードを書き換えてる箇所がございます。主にわかりにくい箇所や間違っている箇所を修正しました。
変化率
pct_change()を使用することで簡単に変化率を取得できます。
まずは、日経平均株価と為替(ドル円)を取得しておきます。今回は、前回の記事で紹介した”pandas-datareader”を使用ます。
import pandas_datareader.data as pdr
import pandas as pd
start = 2000
N225 = pdr.DataReader('^N225', 'yahoo', start) # 日経平均株価
fx = pdr.DataReader('DEXJPUS', 'fred', start) # 為替(ドル/円)次に、2資産のdfを結合し、変化率に変換します。
# データを連結
N_fx = pd.concat([N225.Close, fx], axis=1).dropna()
N_fx.columns = ['N225', 'FX']
# 変化率に変換
N_fx = N_fx.pct_change().dropna()
N_fx.head()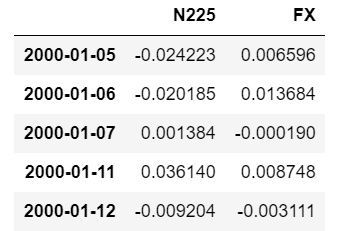
指定した期間幅ごとの統計値(平均や相関係数など)
時系列データ分析では、各時点における直近20日間の平均や分散、相関係数などを計算したいときに使えるのが、rolling(window)です。引数のwindowには、期間幅を指定します。
例えば、各時点で直近20日平均を算出したい場合は、以下の通り。
# 20日営業日ベースでN22の平均を求める
N225.rolling(window=20).mean().dropna()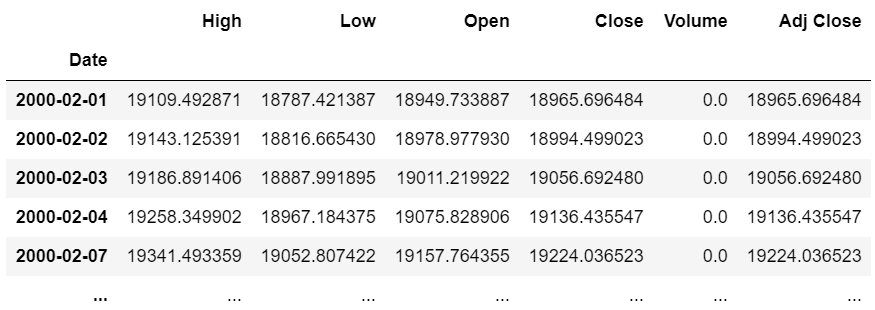
他の統計値を算出したい場合は、mean()を次のものに変えれば計算できます。
最大値:max(), 最小値:min(), 分散:var(), 標準偏差:std()。
次に、各時点で直近20日間の相関係数を算出したい場合は、以下の通り。
# 20日営業日ベースでN225とFXの相関を求める
N225.rolling(window=20).corr(N_fx.FX.rolling(window=20)).dropna()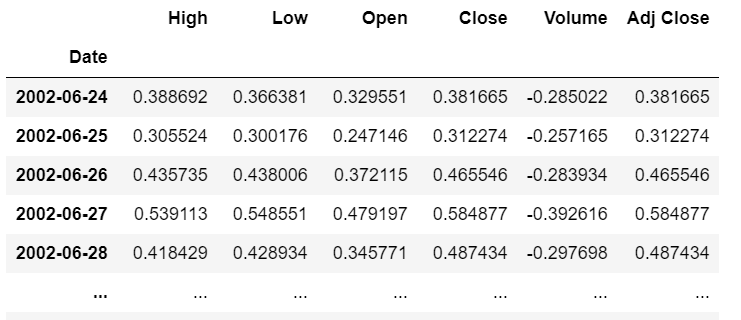
サンプリング期間の変更(日次⇒週次や月次にする)
resample()メソッドを使うとサンプリング期間を変更できます。
例えば、日次のデータを月次に変えたい場合は以下のコードでできます。変換する際は、各月の平均値でリサンプルをしております。
N225.resample('M').mean()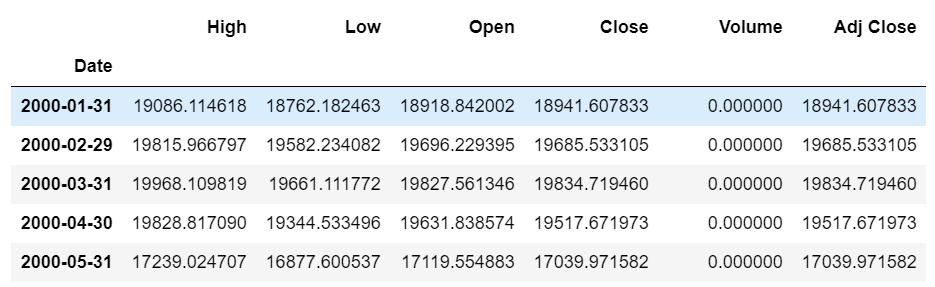
引数を変えることでリサンプル期間を自在に変更できます。
例えば、週次は”W”、2ヵ月毎は”2M”、年次は”Y”に対応しております。
今回は日次のデータを例に紹介しましたが、時間単位でデータに対しても変換可能です。
リサンプルは平均以外でも可能です。mean()の部分を次のものに変えるだけです。
最大値:max()、最小値:min()、期間の最初の値:first()、期間の最後の値:last()。
対数変化率(対数収益率)とボラティリティ(標準偏差)
対数収益率は、numpyのlog()とdataframeのdiff()を用いれば1行で計算できます。標準偏差はdataframのstd()で計算できます。
以下、日経平均株価の対数変化率を求めたコードになります。
import numpy as np np.log(N225.Close).diff().dropna()

ボラティリティは以下の通り。
なお、日次のボラティリティは、sqrt(250)をかけて年次に変換することが良くあります。
N225.std()
移動平均
rolling()を使用すれば、移動平均は簡単に計算できます。
今回は、日経平均株価の終値(Close)250日に関して250日移動平均を計算し、グラフを表示してみます。
import matplotlib.pyplot as plt
# 250日移動平均を計算
ma250 = N225.Close.rolling(250).mean()
# 終値と250日移動平均をプロット
N225.Close.plot(label='N225', style='--')
ma250.plot(label='MA250')
plt.ylabel('N225 index')
plt.legend()移動平均以外にも、移動最大値、移動最小値、移動中央値、移動標準偏差も求めることができます。その場合は、.mean()をそれぞれ、.max()、.min()、.median()、.std()に変更するだけです。
おまけ:基本統計量とボラティリティのクラスタリング
基本統計量
基本統計量は、describe()で算出できます。
金融に限らずデータ分析ではよく使いますのでおまけとして載せておきます。
データ構造を瞬時に見られるので大変便利です。
N225.describe()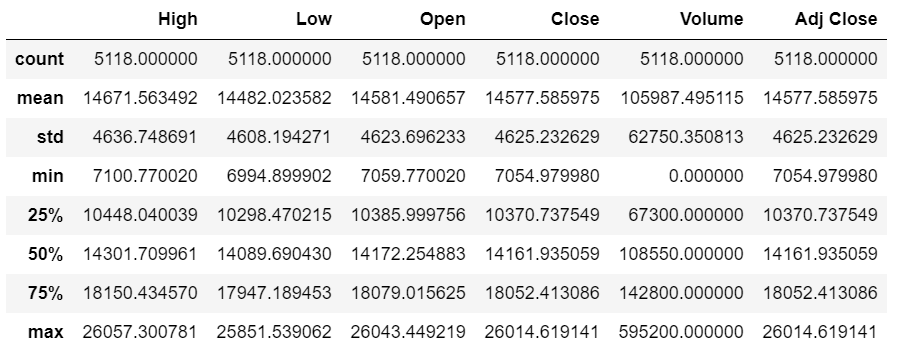
ボラティリティのクラスタリング
ボラティリティは一定ではなく、上下を繰り返して、時として大きくジャンプしてしばらくそこにとどまり、時間が経過すると以前の状態に戻ることがあります。この現象をボラティリティのクラスタリングと言うそうです。
移動標準偏差(250日)を算出し、図示すると以下の通り。
# 対数リターンを算出
R = np.log(N225.Close).diff().dropna()
# 期間幅が250日のボラティリティを計算
sigma = pd.Series.rolling(R, window=250).std() * np.sqrt(250)
# プロット
sigma.plot()
plt.ylabel('standard deviation 250 N225')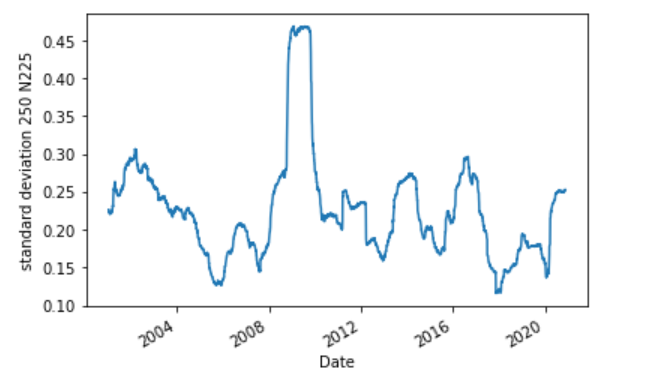
2009年~2011年あたりでボラティリティのクラスタリングが確認されました。
ちょうどリーマンショックの時期に該当してますね。
最後に
今回は、Pythonによる金融データ分析で使えそうな基本的なテクニックを紹介しました。
Pythonでデータ分析する場合は、pandaやnumpのツールをベースに計算したほうが処理の速さ・正確さから良いです。
今回紹介した関数以外にも便利なものはあるので、また別の機会に整理しようと思います。



コメント